त्रिकोणमितीय फलनों की सीमाएं

त्रिकोणमिति, गणित की सबसे महत्वपूर्ण शाखाओं में से एक है। हम जानते हैं कि छह त्रिकोणमितीय फलन हैं और त्रिकोणमितीय की सीमा प्रत्येक त्रिकोणमितीय फलन की सीमा है। हम आसानी से त्रिकोणमितीय फलन की सीमा ज्ञात कर सकते हैं और विचार के बिंदु के साथ दिए गए फलन के आधार पर त्रिकोणमितीय फलन की सीमा उपस्थित हो भी सकती है और नहीं भी।

त्रिकोणमितीय फलन के लिए, हम फलन चर को सीमा मान से बदलकर सभी छह त्रिकोणमितीय फलन की सीमा आसानी से ले सकते हैं। त्रिकोणमितीय फलन की सीमा फलन के प्रांत(डोमेन) और परिसर(रेंज) पर निर्भर करती है। इस लेख में, हम सभी छह त्रिकोणमितीय फलन की सीमा, उनके उदाहरण और अन्य के बारे में विस्तार से जानेंगे।

परिभाषा

त्रिकोणमितीय फलन वह फलन है जो त्रिभुज के कोणों और त्रिभुज की भुजाओं के बीच के संबंध को दर्शाता है। इन्हें वृत्ताकार फलन भी कहा जाता है क्योंकि ये कुछ समय बाद अपने मान को वृत्ताकार तरीके से दोहराते हैं।

गणित में सीमाएँ अद्वितीय वास्तविक संख्याएँ होती हैं। आइए एक वास्तविक-मूल्यवान फलन “$f$” और वास्तविक संख्या “$c$” पर विचार करें, सीमा को सामान्य रूप से $\textstyle \lim _{x\to c}\displaystyle f(x)=L$ के रूप में परिभाषित किया जाता है। इसे “$x$ के $f$ की सीमा, जैसे-जैसे $x$, $c$ के करीब पहुँचता है $L$ के बराबर होता है” के रूप में पढ़ा जाता है। “$lim$” सीमा को दर्शाता है, और तथ्य यह है कि फलन $f(x)$ सीमा $L$ के करीब पहुँचता है क्योंकि $x$, $c$ के करीब पहुँचता है, इसे दाएँ तीर द्वारा वर्णित किया गया है।

त्रिकोणमितीय फलनों की सीमाएँ

त्रिकोणमितीय फलनों की परिमित सीमा, अर्थात् $x$ के परिमित मान के लिए त्रिकोणमितीय फलन की सीमा पर नीचे दी गई तालिका में चर्चा की गई है:

फलन	फलनों की सीमाएँ
sin x	limx⇢asin x = sin a
cos x	limx⇢acos x = cos a
tan x	limx⇢atan x = tan a
cosec x	limx⇢acosec x = cosec a
sec x	limx⇢asec x = sec a
cot x	limx⇢acot x = cot a

जैसा कि ऊपर दी गई तालिका से देखा जा सकता है, यह स्पष्ट है कि त्रिकोणमितीय फलन की परिमित सीमा कुछ अपवादों को छोड़कर परिमित मान में परिणत होती है। हम जानते हैं कि $sinx$ और $cosx$ के लिए उनकी सीमा $-1$ और $1$ के बीच होती है और इसलिए अनंत सीमा के लिए उनका मान $-1$ और $1$ के बीच दोलन करता है, उनका सटीक मान पाना संभव नहीं है और इस प्रकार अनंत पर उनका लिंट अपरिभाषित है। $x$ के धनात्मक या ऋणात्मक अनंत तक पहुँचने के लिए, त्रिकोणमितीय फलन की सीमा पर नीचे चर्चा की गई है।

त्रिकोणमितीय फलन की सीमाओं के प्रमेय

हमारे पास दो प्रमेय हैं जिनका उपयोग त्रिकोणमितीय फलन की सीमा को परिभाषित करने में किया जाता है, जो हैं,

प्रमेय 1

किसी भी दो वास्तविक-मूल्यवान फलन $f(x)$ और$g(x)$ के लिए जो एक ही प्रांत में परिभाषित हैं और उनके बीच संबंध $f(x)\leq g(x)$ है। हम इन फलन की सीमा को $x$ पर ले सकते हैं जो a के करीब है, फिर,

$\textstyle \lim _{x\to a}\displaystyle f(x)=f(a)$ और, $\textstyle \lim _{x\to a}\displaystyle g(x)=g(a)$

यदि दोनों सीमाएँ उपस्थित हैं तो हम आसानी से कह सकते हैं कि,

$\textstyle \lim _{x\to a}\displaystyle f(x)\leq g(x)$

प्रमेय 2 (सैंडविच प्रमेय)

इस प्रमेय का उपयोग उन फलन की सीमा की गणना करने के लिए किया जाता है जिनकी सीमा की गणना आसानी से नहीं की जा सकती है जैसे $(x=0)$ पर ${\frac {sinx}{x}}$। फलन $g(x)$ को दो फलन $h(x)$ और $g(x)$ के बीच इस तरह से दबाया या सैंडविच किया जाता है कि

$\displaystyle f(x)\leq g(x)\leq h(x)$

उपरोक्त स्थिति का आलेख नीचे दिखाया गया है जो सैंडविच प्रमेय सीमा को दर्शाता है।

हम कह सकते हैं कि $h(x)$, $g(x)$ की ऊपरी सीमा है और $h(x)$ बिंदु $a$ पर इसकी निचली सीमा है जैसा कि ऊपर दिए गए आलेख में देखा जा सकता है:

$\textstyle \lim _{x\to a}\displaystyle h(x)=L$ and $\textstyle \lim _{x\to a}\displaystyle f(x)=L$

जहाँ, $a$ वह बिंदु है जिस पर सीमा की गणना की जाती है, और $L$ सीमा का मान है।

तब,

$\textstyle \lim _{x\to a}\displaystyle g(x)=L$

उदाहरण

दिया गया: $g(x)=x^{2}sin{\Bigl (}{\frac {1}{x}}{\Bigr )}$, ज्ञात करें: $\textstyle \lim _{x\to 0}\displaystyle g(x)$

समाधान:

हम जानते हैं,

$-1\leq sin\left({\frac {1}{x}}\right)\leq 1$ इसके प्रांतके अंतर्गत

$x^{2}$ से गुणा करना

$-x^{2}\leq x2sin\left({\frac {1}{x}}\right)\leq x^{2}$

फिर मान लें कि $f(x)=-x^{2}$और $h(x)=x^{2}$

$\displaystyle f(x)\leq g(x)\leq h(x)$

सैंडविच प्रमेय का उपयोग करते हुए,

चूँकि $\textstyle \lim _{x\to a}\displaystyle h(x)=\textstyle \lim _{x\to a}\displaystyle f(x)=L$

इसलिए,

$\textstyle \lim _{x\to a}\displaystyle g(x)=L$

$\Rightarrow \textstyle \lim _{x\to 0}\displaystyle f(x)=\textstyle \lim _{x\to 0}\displaystyle -x^{2}=0$ और

$\Rightarrow \textstyle \lim _{x\to 0}\displaystyle h(x)=\textstyle \lim _{x\to 0}\displaystyle x^{2}=0$

इस प्रकार, $\textstyle \lim _{x\to 0}\displaystyle g(x)=0$

विभिन्न त्रिकोणमितीय फलनों की सीमाएँ

जैसा कि हम जानते हैं कि हमारे पास छह त्रिकोणमितीय फलन हैं, अर्थात्,

1. साइन
2. कोसाइन
3. स्पर्शरेखा
4. सेकेंट
5. कोसेकेंट
6. कोटेंजेंट

नीचे दिए गए लेख में प्रत्येक फलन की सीमा पर विस्तार से चर्चा की गई है।

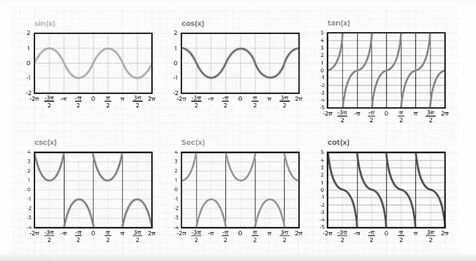
साइन फलन की सीमा

फलन $f(x)=sin(x)$ अपने पूरे डोमेन पर एक सतत फलन है, जिसका डोमेन सभी वास्तविक संख्याओं से मिलकर बना है। इस फलन की सीमा $[-1,1]$ है जैसा कि नीचे दिए गए ग्राफ़ में देखा जा सकता है

इसलिए, यदि साइन फलन की सीमा किसी भी दी गई वास्तविक संख्या पर गणना की जाती है तो यह हमेशा परिभाषित होती है और $[-1,1]$ के बीच होती है।

मान लेते हैं कि , $f(x)=sin(x)$

$\textstyle \lim _{x\to a}\displaystyle f(x)=\textstyle \lim _{x\to a}sin(x)$

$\Rightarrow \textstyle \lim _{x\to a}\displaystyle f(x)=sin(a)$,      (जहाँ $a$ एक वास्तविक संख्या है)

कोसाइन फलन की सीमा

फलन $f(x)=cos(x)$ अपने पूरे डोमेन पर एक सतत फलन है, जिसका डोमेन सभी वास्तविक संख्याओं से मिलकर बना है।

इस फलन की सीमा $[-1,1]$ है जैसा कि नीचे दिए गए ग्राफ़ में देखा जा सकता है।

इसलिए, यदि कोसाइन फलन की सीमा किसी भी दी गई वास्तविक संख्या पर गणना की जाती है तो यह हमेशा परिभाषित होती है और $[-1,1]$ के बीच होती है।

मान लेते हैं कि, $g(x)=cos(x)$

$\textstyle \lim _{x\to a}\displaystyle g(x)=\textstyle \lim _{x\to a}cos(x)$

$\Rightarrow \textstyle \lim _{x\to a}\displaystyle g(x)=cos(a)$,      (जहाँ $a$ एक वास्तविक संख्या है)

स्पर्शरेखा फलन की सीमा

फलन f(x) = tan(x) सभी वास्तविक संख्याओं पर परिभाषित है, सिवाय उन मानों के जहाँ cos(x) 0 के बराबर है, अर्थात सभी पूर्णांक n के लिए π/2 + πn के मान। इस प्रकार, इसका डोमेन π/2 + πn, n € Z को छोड़कर सभी वास्तविक संख्याएँ हैं।

इस फलन की सीमा (-∞, +c) है जैसा कि नीचे दिए गए ग्राफ़ में देखा जा सकता है।

इसलिए, यदि स्पर्शरेखा फलन की सीमा की गणना उसके डोमेन में की जाती है तो यह हमेशा परिभाषित होती है और (-∞, +∞) के बीच होती है।

f(x) = tan(x)

limx→a f(x) = limx→a  tan(x)

⇒ lim_x→a f(x) = tan(a)                 (where a belongs to real no. except π/2 + πn, n € Z)

कोसेक फलन की सीमा

फलन f(x) = cosec(x) सभी वास्तविक संख्याओं पर परिभाषित है, सिवाय उन मानों के जहाँ sin(x) 0 के बराबर है, अर्थात सभी पूर्णांक n के लिए πn का मान। इस प्रकार, इसका डोमेन πn, n € Z को छोड़कर सभी वास्तविक संख्याएँ हैं।

इस फलन की सीमा (-∞,-1] U [1,+∞) है जैसा कि नीचे दिए गए ग्राफ़ में देखा जा सकता है।

इसलिए, यदि कोसाइन फलन की सीमा की गणना उसके डोमेन में की जाती है तो यह हमेशा परिभाषित होती है और इसकी सीमा के बीच होती है।

मान लेते हैं कि, f(x) = cosec(x)

limx→a f(x) = limx→a cosec(x)

⇒ limx→a f(x) = cosec(a)        (where a∈ R – nπ: n € Z)

सेकेंट फलन की सीमा

फलन f(x) = sec(x) सभी वास्तविक संख्याओं पर परिभाषित है, सिवाय उन मानों के जहाँ cos(x) 0 के बराबर है, अर्थात सभी पूर्णांक n के लिए π/2 + πn के मान। इस प्रकार, इसका डोमेन π/2 + πn, n € Z को छोड़कर सभी वास्तविक संख्याएँ हैं।

इस फलन की सीमा (-∞, -1] U [1, +∞) है जैसा कि नीचे दिए गए ग्राफ़ में देखा जा सकता है।

इसलिए, यदि सेक फलन की सीमा की गणना उसके डोमेन में की जाती है तो यह हमेशा परिभाषित होती है और इसकी सीमा के बीच होती है।

मान लेते हैं कि, f(x) = sec(x)

limx→a f(x) = limx→a sec(x)

⇒ lim_x→a f(x) = sec(a)          (where a∈ R – {nπ + π/2}: n € Z)

कॉट फलन की सीमा

फलन f(x) = cot(x) सभी वास्तविक संख्याओं पर परिभाषित है, सिवाय उन मानों के जहाँ tan(x) 0 के बराबर है, अर्थात सभी पूर्णांक n के लिए πn का मान। इस प्रकार, इसका डोमेन πn, n € Z को छोड़कर सभी वास्तविक संख्याएँ हैं।

इस फलन की सीमा (-∞, +∞) है जैसा कि नीचे दिए गए ग्राफ़ में देखा जा सकता है।

इसलिए, यदि कॉट फलन की सीमा की गणना उसके डोमेन में की जाती है तो यह हमेशा परिभाषित होती है और इसकी सीमा के बीच होती है।

मान लेते हैं कि, f(x) = cot(x)

limx→a f(x) = limx→a cot(x)

⇒ lim_x→a f(x) = cot(a)               (where a∈ R – nπ: n € Z)

विभिन्न त्रिकोणमितीय फलनों का आलेख

विभिन्न त्रिकोणमितीय फलन का आलेख निम्नलिखित छवि में जोड़ा गया है:

चित्र- विभिन्न त्रिकोणमितीय फलन का आलेख