रेखा के दिक्-कोज्या व दिक्- अनुपात: Difference between revisions

Latest revision as of 11:53, 16 December 2024

दिक्- कोज्या ,त्रि-आयामी अंतरिक्ष में रेखा द्वारा क्रमशः $x$ -अक्ष, $y$ -अक्ष, $z$ -अक्ष के साथ बनाए गए कोण का कोज्या है। दिक्- कोज्या की गणना त्रि-आयामी अंतरिक्ष में एक सदिश या एक सरल रेखा के लिए की जा सकती है। यह त्रि- अक्षों के साथ रेखा द्वारा बनाए गए कोण का कोज्या है।

दिक्-अनुपात तीन अक्षों, $x$ -अक्ष, $y$ -अक्ष और $z$ -अक्ष के संदर्भ में एक रेखा या सदिश के घटकों को जानने में सहायता करता है। एक सदिश ${\overrightarrow {A}}=a{\overset {\frown }{i}}+b{\overset {\frown }{j}}+c{\overset {\frown }{k}}$ के लिए दिक्- अनुपात क्रमशः $a,b$ और $c$ हैं। दिक्- अनुपात, दिक्- कोज्या , दो रेखाओं के बीच का कोण या दो सदिशों का डॉट गुणनफल ज्ञात करने में सहायता करते हैं।

आइए दिक्- कोज्या, दिक्- अनुपात , दिक्- कोज्या के साथ दिक्- अनुपात के संबंध और दिक्- अनुपातों के उपयोगों और त्रि-आयामी अंतरिक्ष में दो बिंदुओं को जोड़ने वाली रेखा के दिक्- कोज्या के बारे में अधिक जानें।

दिक्-कोज्या

दिक्- कोज्या परिभाषा

दिक्- कोज्या, त्रि- आयामी अंतरिक्ष में एक सदिश या रेखा का संबंध त्रि- अक्षों में से प्रत्येक के साथ देता है। दिक्- कोज्या इस रेखा द्वारा क्रमशः $x$ -अक्ष, $y$ -अक्ष और $z$ -अक्ष के साथ अंतरित कोण का कोज्या है। यदि रेखा द्वारा तीनों अक्षों के साथ अंतरित कोण $\alpha$ , $\beta$ और $\gamma$ हैं, तो दिक्- कोज्या क्रमशः $Cos\alpha ,Cos\beta ,Cos\gamma$ हैं।

एक सदिश ${\overrightarrow {A}}=a{\overset {\frown }{i}}+b{\overset {\frown }{j}}+c{\overset {\frown }{k}}$ के लिए दिक्- कोज्या $Cos\alpha ={\frac {a}{\sqrt {a^{2}+b^{2}+c^{2}}}},\ Cos\beta ={\frac {b}{\sqrt {a^{2}+b^{2}+c^{2}}}},\ Cos\gamma ={\frac {c}{\sqrt {a^{2}+b^{2}+c^{2}}}}$

हैं।

दिक्- कोज्या को $l,m,n$ द्वारा भी दर्शाया जाता है और हम प्रायः दिक्- कोज्या को इस प्रकार दर्शाते हैं $l={\frac {a}{\sqrt {a^{2}+b^{2}+c^{2}}}},m={\frac {b}{\sqrt {a^{2}+b^{2}+c^{2}}}},n={\frac {c}{\sqrt {a^{2}+b^{2}+c^{2}}}}$ l त्रि-आयामी अंतरिक्ष में एक बिंदु $A(a,b,c)$ के लिए दिक्- कोज्या इस बिंदु को मूल $O$ से जोड़ने वाली रेखा की दिक्- कोज्या है। रेखा $OA$ की दिक्- कोज्या है l $l={\frac {a}{\sqrt {a^{2}+b^{2}+c^{2}}}},m={\frac {b}{\sqrt {a^{2}+b^{2}+c^{2}}}},n={\frac {c}{\sqrt {a^{2}+b^{2}+c^{2}}}}$

दिक्-अनुपात परिभाषा

दिक्- अनुपात क्रमशः $x$ -अक्ष, $y$ -अक्ष, $z$ -अक्ष के साथ एक सदिश के घटक होते हैं। एक सदिश के दिक्- अनुपात ${\overrightarrow {A}}=a{\overset {\frown }{i}}+b{\overset {\frown }{j}}+c{\overset {\frown }{k}}$ क्रमशः $(a,b,c)$ हैं, और ये मान क्रमशः $x$ -अक्ष, $y$ -अक्ष और $z$ -अक्ष के साथ सदिश के घटक मानों का प्रतिनिधित्व करते हैं। दिक्- अनुपात की संख्या अंतरिक्ष के आयाम पर निर्भर करती है। द्वि-आयामी अंतरिक्ष में एक रेखा के लिए, दो दिक्- अनुपात होते हैं, और त्रि-आयामी अंतरिक्ष में एक रेखा के लिए, तीन दिक्- अनुपात होते हैं।

सदिश: ${\overrightarrow {A}}=a{\overset {\frown }{i}}+b{\overset {\frown }{j}}+c{\overset {\frown }{k}}$

दिक्-अनुपात: $a,b,c$

दो बिंदुओं $(x_{1},y_{1},z_{1})$ और $(x_{2},y_{2},z_{2})$ को जोड़ने वाली एक सदिश रेखा के दिक्- अनुपात $(x_{2}-x_{1},y_{2}-y_{1},z_{2}-z_{1})$ हैं। दिक्- अनुपात किसी रेखा की दिक्- कोज्या ज्ञात करने के लिए उपयोगी होते हैं। किसी दी गई रेखा के लिए दिक्- अनुपातों का एक अनंत समुच्चय हो सकता है, और दो समानांतर रेखाओं के दिक्- अनुपात समानुपात में होते हैं।

दिक्- अनुपात का उपयोग

दिक्- अनुपात का उपयोग दो सदिशों की तुलना करने के लिए किया जाता है। दो समांतर सदिशों के दिक्- अनुपात समानुपात में होते हैं। दो सदिशों ${\overrightarrow {A}}=a_{1}{\overset {\frown }{i}}+b_{1}{\overset {\frown }{j}}+c_{1}{\overset {\frown }{k}},\ a_{2}{\overset {\frown }{i}}+b_{2}{\overset {\frown }{j}}+c_{2}{\overset {\frown }{k}},$ , के लिए दिक्- अनुपात ${\frac {a_{1}}{a_{2}}}={\frac {b_{1}}{b_{2}}}={\frac {c_{1}}{c_{2}}}$ हैं।

दिक्- अनुपात दो सदिशों का डॉट गुणनफल ज्ञात करने के लिए उपयोगी है। दो सदिशों का डॉट गुणनफल दो सदिशों के संबंधित दिक्- अनुपातों के गुणनफल का योग है। दो सदिशों ${\overrightarrow {A}}=a_{1}{\overset {\frown }{i}}+b_{1}{\overset {\frown }{j}}+c_{1}{\overset {\frown }{k}},\ a_{2}{\overset {\frown }{i}}+b_{2}{\overset {\frown }{j}}+c_{2}{\overset {\frown }{k}},$ के लिए सदिशों का डॉट गुणनफल ${\overrightarrow {A}}\cdot {\overrightarrow {B}}=a_{1}\cdot a_{2}+b_{1}\cdot b_{2}+c_{1}\cdot c_{2}$ है।

दिक्- अनुपात दो सदिशों के बीच के कोण को ज्ञात करने में सहायक है। दो सदिशों के बीच के कोण के $cos$ की गणना दो सदिशों के डॉट गुणनफल को लेकर और उसे दो सदिशों के परिमाण के गुणनफल से विभाजित करके आसानी से की जा सकती है। दो सदिशों ${\overrightarrow {A}}=a_{1}{\overset {\frown }{i}}+b_{1}{\overset {\frown }{j}}+c_{1}{\overset {\frown }{k}},\ a_{2}{\overset {\frown }{i}}+b_{2}{\overset {\frown }{j}}+c_{2}{\overset {\frown }{k}},$ के लिए दो सदिशों के बीच का कोण $Cos\theta ={\frac {a_{1}\cdot a_{2}+b1\cdot b_{2}+c_{1}\cdot c_{2}}{{\sqrt {a_{1}^{2}+b_{1}^{2}+c_{1}^{2}}}\cdot {\sqrt {a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}}}$ है।

दिक्- अनुपात और दिक्- कोज्या के बीच संबंध

दिक्- अनुपात एक रेखा की दिक्- कोज्या ज्ञात करने में सहायता करते हैं। दिक्- कोज्या इस रेखा द्वारा क्रमशः $x$ -अक्ष, $y$ -अक्ष और $z$ -अक्ष के साथ अंतरित कोण की कोज्या है। यदि रेखा द्वारा तीनों अक्षों के साथ अंतरित कोण $\alpha$ , $\beta$ और $\gamma$ हैं, तो दिक्- कोज्या क्रमशः $Cos\alpha ,Cos\beta ,Cos\gamma$ हैं।

दिक्- अनुपात $a,b,c$ वाले सदिश ${\overrightarrow {A}}=a{\overset {\frown }{i}}+b{\overset {\frown }{j}}+c{\overset {\frown }{k}}$ के लिए दिक्- कोज्या $Cos\alpha ={\frac {a}{\sqrt {a^{2}+b^{2}+c^{2}}}},\ Cos\beta ={\frac {b}{\sqrt {a^{2}+b^{2}+c^{2}}}},\ Cos\gamma ={\frac {c}{\sqrt {a^{2}+b^{2}+c^{2}}}}$ है।

दिक्- कोज्या को $l,m,n$ द्वारा भी दर्शाया जाता है और हम अक्सर दिक्- कोज्या को l $l={\frac {a}{\sqrt {a^{2}+b^{2}+c^{2}}}},m={\frac {b}{\sqrt {a^{2}+b^{2}+c^{2}}}},n={\frac {c}{\sqrt {a^{2}+b^{2}+c^{2}}}}$ के रूप में दर्शाते हैं।

यहाँ हमl $l=Cos\alpha ,m=Cos\beta ,n=Cos\gamma$ मानते हैं। इसलिए हमारे पास दिक्- कोज्या के बीच संबंध $l^{2}+m^{2}+n^{2}=1$ है।

उदाहरण

उदाहरण 1: बिंदु $(-4,2,3)$ को मूल बिंदु से मिलाने वाली रेखा की दिक्- कोज्या ज्ञात करें।

समाधान:

मूल बिंदु $(0,0,0)$ और बिंदु $(-4,2,3)$ को मिलाने वाली रेखा के लिए दिक्- अनुपात $-4,2,3$ हैं।

रेखा का परिमाण $={\sqrt {(-4)^{2}+2^{2}+3^{2})}}={\sqrt {29}}$

इसलिए दिक्- कोज्या $(-4/{\sqrt {29}},2/{\sqrt {29}},3/{\sqrt {29}})$ हैं।

उदाहरण 2: किसी बिंदु के स्थिति सदिश का दिक्- अनुपात ज्ञात करें ${\overrightarrow {OA}}=4{\overset {\frown }{i}}-3{\overset {\frown }{j}}+2{\overset {\frown }{k}}$

समाधान:

दिया गया सदिश ${\overrightarrow {OA}}=4{\overset {\frown }{i}}-3{\overset {\frown }{j}}+2{\overset {\frown }{k}}$ है ।

दिक्- अनुपात $=(4,-3,2)$

@@ Line 1: / Line 1: @@
-Direction Cosines and Direction Ratios of a Line
+दिक्- कोज्या  ,त्रि-आयामी अंतरिक्ष में रेखा द्वारा क्रमशः <math>x</math>-अक्ष, <math>y</math>-अक्ष, <math>z</math>-अक्ष के साथ बनाए गए कोण का कोज्या है। दिक्- कोज्या   की गणना त्रि-आयामी अंतरिक्ष में एक सदिश या एक सरल [[रेखा]] के लिए की जा सकती है। यह त्रि- अक्षों के साथ रेखा द्वारा बनाए गए कोण का कोज्या   है।
+दिक्-अनुपात तीन अक्षों, <math>x</math>-अक्ष, <math>y</math>-अक्ष और <math>z</math>-अक्ष के संदर्भ में एक रेखा या सदिश के घटकों को जानने में सहायता करता है। एक सदिश <math>\overrightarrow{A}=a\overset{\frown}{i}+b\overset{\frown}{j}+c \overset{\frown}{k} </math> के लिए दिक्- अनुपात क्रमशः<math>a, b</math> और <math>c</math> हैं। दिक्- अनुपात, दिक्- कोज्या , दो रेखाओं के बीच का कोण या दो सदिशों का डॉट गुणनफल ज्ञात करने में सहायता करते हैं।
+आइए दिक्- कोज्या, दिक्- अनुपात , दिक्- कोज्या के साथ दिक्- अनुपात के संबंध और दिक्- अनुपातों के उपयोगों  और त्रि-आयामी अंतरिक्ष में दो बिंदुओं को जोड़ने वाली रेखा के दिक्- कोज्या के बारे में अधिक जानें।
+[[File:दिक्-कोसाइन.jpg|thumb|दिक्-कोज्या  |251x251px]]
+== दिक्- कोज्या परिभाषा ==
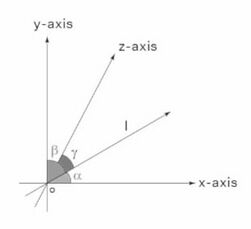
+[[दिक्-कोसाइन|दिक्- कोज्या]], त्रि- आयामी अंतरिक्ष में एक [[सदिश गुणन|सदिश]] या रेखा का संबंध त्रि- अक्षों में से प्रत्येक के साथ देता है। दिक्- कोज्या  इस रेखा द्वारा क्रमशः <math>x</math>-अक्ष, <math>y</math>-अक्ष और <math>z</math>-अक्ष के साथ अंतरित कोण का कोज्या  है। यदि रेखा द्वारा तीनों अक्षों के साथ अंतरित कोण <math>\alpha</math>, <math>\beta</math>और <math>\gamma</math> हैं, तो दिक्- कोज्या  क्रमशः <math>Cos\alpha, Cos\beta, Cos\gamma</math> हैं।
+एक सदिश <math>\overrightarrow{A}=a\overset{\frown}{i}+b\overset{\frown}{j}+c \overset{\frown}{k} </math>  के लिए दिक्- कोज्या   <math> Cos\alpha = \frac{a}{\sqrt{a^2+b^2+c^2}}, \ Cos\beta = \frac{b}{\sqrt{a^2+b^2+c^2}}, \ Cos\gamma = \frac{c}{\sqrt{a^2+b^2+c^2}}</math>
+हैं।
+दिक्- कोज्या  को <math>l, m, n</math> द्वारा भी दर्शाया जाता है और हम प्रायः दिक्- कोज्या को इस प्रकार दर्शाते हैं <math>l= \frac{a}{\sqrt{a^2+b^2+c^2}}, m = \frac{b}{\sqrt{a^2+b^2+c^2}}, n = \frac{c}{\sqrt{a^2+b^2+c^2}}</math> l  त्रि-आयामी अंतरिक्ष में एक बिंदु <math>A (a, b, c)</math>के लिए दिक्- कोज्या   इस बिंदु को मूल <math>O</math> से जोड़ने वाली रेखा की दिक्- कोज्या  है। रेखा <math>OA</math> की दिक्- कोज्या है  l <math>l= \frac{a}{\sqrt{a^2+b^2+c^2}}, m = \frac{b}{\sqrt{a^2+b^2+c^2}}, n = \frac{c}{\sqrt{a^2+b^2+c^2}}</math>
+== दिक्-अनुपात परिभाषा ==
+दिक्- अनुपात क्रमशः <math>x</math>-अक्ष, <math>y</math>-अक्ष, <math>z</math>-अक्ष के साथ एक सदिश के घटक होते हैं। एक सदिश के दिक्- अनुपात  <math>\overrightarrow{A}=a\overset{\frown}{i}+b\overset{\frown}{j}+c \overset{\frown}{k} </math> क्रमशः <math>(a, b, c) </math> हैं, और ये मान क्रमशः <math>x</math>-अक्ष, <math>y</math>-अक्ष और <math>z</math>-अक्ष के साथ सदिश के घटक मानों का प्रतिनिधित्व करते हैं। दिक्- अनुपात की संख्या अंतरिक्ष के आयाम पर निर्भर करती है। द्वि-आयामी अंतरिक्ष में एक रेखा के लिए, दो दिक्- अनुपात होते हैं, और त्रि-आयामी अंतरिक्ष में एक रेखा के लिए, तीन दिक्- अनुपात होते हैं।
+'''सदिश: <math>\overrightarrow{A}=a\overset{\frown}{i}+b\overset{\frown}{j}+c \overset{\frown}{k} </math>'''
+'''दिक्-अनुपात:'''   <math>a, b, c </math>
+दो बिंदुओं <math>(x_1,y_1,z_1) </math> और <math>(x_2,y_2,z_2) </math> को जोड़ने वाली एक सदिश रेखा के दिक्- अनुपात <math>(x_2-x_1,y_2-y_1,z_2-z_1) </math> हैं। दिक्-  अनुपात किसी रेखा की दिक्- कोज्या ज्ञात करने के लिए उपयोगी होते हैं। किसी दी गई रेखा के लिए दिक्- अनुपातों का एक अनंत समुच्चय हो सकता है, और दो समानांतर रेखाओं के दिक्- अनुपात समानुपात में होते हैं।
+== दिक्- अनुपात का उपयोग ==
+दिक्- अनुपात का उपयोग दो सदिशों की तुलना करने के लिए किया जाता है। दो समांतर सदिशों के दिक्- अनुपात समानुपात में होते हैं। दो सदिशों '''<math>\overrightarrow{A}=a_1\overset{\frown}{i}+b_1\overset{\frown}{j}+c_1 \overset{\frown}{k},\ a_2 \overset{\frown}{i}+b_2\overset{\frown}{j}+c_2 \overset{\frown}{k}, </math>''', के लिए दिक्- अनुपात <math>\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2} </math> हैं।
+दिक्-  अनुपात दो सदिशों का डॉट गुणनफल ज्ञात करने के लिए उपयोगी है। दो सदिशों का डॉट गुणनफल दो सदिशों के संबंधित दिक्-  अनुपातों के गुणनफल का योग है। दो सदिशों  '''<math>\overrightarrow{A}=a_1\overset{\frown}{i}+b_1\overset{\frown}{j}+c_1 \overset{\frown}{k},\ a_2 \overset{\frown}{i}+b_2\overset{\frown}{j}+c_2 \overset{\frown}{k}, </math>'''  के लिए सदिशों का डॉट गुणनफल <math>\overrightarrow{A}\cdot \overrightarrow{B}=a_1\cdot a_2+b_1\cdot b_2+c_1\cdot c_2 </math> है।
+दिक्-  अनुपात दो सदिशों के बीच के कोण को ज्ञात करने में सहायक है। दो सदिशों के बीच के कोण के <math>cos </math> की गणना दो सदिशों के डॉट गुणनफल को लेकर और उसे दो सदिशों के परिमाण के गुणनफल से विभाजित करके आसानी से की जा सकती है। दो सदिशों '''<math>\overrightarrow{A}=a_1\overset{\frown}{i}+b_1\overset{\frown}{j}+c_1 \overset{\frown}{k},\ a_2 \overset{\frown}{i}+b_2\overset{\frown}{j}+c_2 \overset{\frown}{k}, </math>''' के लिए दो सदिशों के बीच का कोण <math>Cos\theta=\frac{a_1\cdot a_2+b1\cdot b_2+c_1\cdot c_2}{\sqrt{a^2_1+b^2_1+c^2_1}\cdot \sqrt{a^2_2+b^2_2+c^2_2 }} </math>है।
+== दिक्- अनुपात और दिक्- कोज्या के बीच संबंध ==
+दिक्-  अनुपात एक रेखा की दिक्-  कोज्या ज्ञात करने में सहायता करते हैं। दिक्-  कोज्या इस रेखा द्वारा क्रमशः <math>x</math>-अक्ष, <math>y</math>-अक्ष और <math>z</math>-अक्ष के साथ अंतरित कोण की कोज्या है। यदि रेखा द्वारा तीनों अक्षों के साथ अंतरित कोण  <math>\alpha</math>, <math>\beta</math>और <math>\gamma</math> हैं, तो दिक्-  कोज्या क्रमशः <math>Cos\alpha, Cos\beta, Cos\gamma</math> हैं।
+दिक्- अनुपात <math>a, b, c </math> वाले सदिश '''<math>\overrightarrow{A}=a\overset{\frown}{i}+b\overset{\frown}{j}+c \overset{\frown}{k} </math>'''  के लिए दिक्-  कोज्या <math> Cos\alpha = \frac{a}{\sqrt{a^2+b^2+c^2}}, \ Cos\beta = \frac{b}{\sqrt{a^2+b^2+c^2}}, \ Cos\gamma = \frac{c}{\sqrt{a^2+b^2+c^2}}</math>  है।
+दिक्-  कोज्या को <math>l, m, n</math>  द्वारा भी दर्शाया जाता है और हम अक्सर दिक्-  कोज्या को l<math>l= \frac{a}{\sqrt{a^2+b^2+c^2}}, m = \frac{b}{\sqrt{a^2+b^2+c^2}}, n = \frac{c}{\sqrt{a^2+b^2+c^2}}</math>  के रूप में दर्शाते हैं।
+यहाँ हमl<math>l = Cos\alpha, m = Cos\beta, n = Cos\gamma</math> मानते हैं। इसलिए हमारे पास दिक्- कोज्या के बीच संबंध <math>l^2 + m^2 + n^2 = 1 </math> है।
+== उदाहरण ==
+'''उदाहरण''' '''1''': बिंदु <math>(-4, 2, 3)</math> को मूल बिंदु से मिलाने वाली रेखा की दिक्- कोज्या ज्ञात करें।
+'''समाधान''':
+मूल बिंदु <math>(0, 0, 0)</math>और बिंदु <math>(-4, 2, 3)</math> को मिलाने वाली रेखा के लिए दिक्- अनुपात <math>-4, 2, 3</math> हैं।
+रेखा का परिमाण <math>=\sqrt{(-4)^2+2^2+3^2)}=\sqrt{29}</math>
+इसलिए दिक्- कोज्या <math>(-4/\sqrt{29}, 2/\sqrt{29}, 3/\sqrt{29})</math> हैं।
+इसलिए दिक्- कोज्या <math>(-4/\sqrt{29}, 2/\sqrt{29}, 3/\sqrt{29})</math> हैं।
+'''उदाहरण 2:''' किसी बिंदु के स्थिति सदिश का दिक्-  अनुपात ज्ञात करें  <math>\overrightarrow{OA}=4\overset{\frown}{i}-3\overset{\frown}{j}+2\overset{\frown}{k}</math>
+'''समाधान''':
+दिया गया सदिश  <math>\overrightarrow{OA}=4\overset{\frown}{i}-3\overset{\frown}{j}+2\overset{\frown}{k}</math>  है ।
+दिक्- अनुपात<math>= (4, -3, 2)</math>
 [[Category:त्रि-विमीय ज्यामिति]][[Category:गणित]][[Category:कक्षा-12]]