एक वृत्त के चाप द्वारा अंतरित कोण: Difference between revisions

Latest revision as of 19:23, 17 September 2024

हमे ज्ञात है कि वृत्त के व्यास के अतिरिक्त किसी जीवा के अंतिम बिंदु उसे दो चापों में विभाजित करते हैं, जिन्हें दीर्घ चाप और लघु चाप कहते हैं। इस लेख में हम वृत्त के चाप द्वारा अंतरित कोण से संबंधित प्रमेय और उसके पूर्ण स्पष्टीकरण के साथ उसके प्रमाण पर चर्चा करेंगे।

एक वृत्त के चाप द्वारा अंतरित कोण – प्रमेय एवं प्रमाण

प्रमेय:

एक चाप द्वारा केंद्र पर बनाया गया कोण वृत्त के शेष भाग पर किसी भी बिंदु पर बनाए गए कोण का दोगुना होता है।

प्रमाण:

केंद्र $O$ वाले एक वृत्त पर विचार करें। यहाँ वृत्त का चाप $PQ$ केंद्र $O$ पर कोण $\angle POQ$ तथा वृत्त के शेष भाग पर स्थित बिंदु $A$ पर कोण $\angle PAQ$ अंतरित करता है।

प्रमाण करने हेतु : $\angle POQ=2\angle PAQ$

इसे प्रमाणित करने के लिए, $AO$ को जोड़ें और इसे बिंदु $B$ तक विस्तारित करें

इस प्रमेय को सिद्ध करते समय दो सामान्य स्थितियाँ हैं।

स्थिति 1:

चित्र -1

त्रिभुज $APO$ पर विचार करें

यहाँ, $OA=OP$ (त्रिज्या)

चूँकि समान भुजाओं के विपरीत कोण समान होते हैं,

$\angle OPA=\angle OAP....(1)$

इसके अतिरिक्त, बाह्य कोण गुण (बाह्य कोण आंतरिक विपरीत कोणों का योग है) का उपयोग करते हुए,

हम लिख सकते हैं,

$\angle BOP=\angle OAP+\angle OPA$

$(1)$ का उपयोग करके

$\angle BOP=\angle OAP+\angle OAP$

$\angle BOP=2\angle OAP....(2)$

इसी प्रकार, एक अन्य त्रिभुज $AQO$ पर विचार करें ,

$OA=OQ$ (त्रिज्या)

चूँकि समान भुजाओं के विपरीत कोण समान होते हैं,

$\angle OQA=\angle OAQ....(3)$

इसी प्रकार, बाह्य कोण गुण का उपयोग करके, हम $\angle BOQ=\angle OAQ+\angle OQA$ प्राप्त करते हैं

$\angle BOQ=\angle OAQ+\angle OAQ$ ( $(3)$ का उपयोग करते हुए)

$\angle BOQ=2\angle OAQ....(4)$

$(2)$ और $(4)$ को जोड़ने पर हमें प्राप्त होता है

$\angle BOP+\angle BOQ=2\angle OAP+2\angle OAQ$

$\angle POQ=2(\angle OAP+\angle OAQ)$

$\angle POQ=2\angle PAQ$

अतः, स्थिति (1) सिद्ध होती है।

स्थिति 2:

चित्र -2

इस स्थिति में $\angle POQ=2\angle PAQ$ को प्रमाणित करने के लिए, हम स्थिति (1) के समान ही चरणों का पालन कर सकते हैं। लेकिन (2) और (4) को जोड़ते समय हमें नीचे दिए गए चरणों का पालन करना होगा।

$\angle BOP+\angle BOQ=2\angle OAP+2\angle OAQ$

प्रतिवर्ती कोण $\angle POQ=2(\angle OAP+\angle OAQ)$ (चूँकि, $PQ$ एक दीर्घ चाप है)

प्रतिवर्ती कोण $\angle POQ=2\angle PAQ$ .

अतः सिद्ध हुआ।

@@ Line 1: / Line 1: @@
-We know that the end points of a chord other than the diameter of a circle divides it into two arcs, namely the major arc and the minor arc.  In this article, we will discuss the theorem related to the angle subtended by an arc of a circle and its proof with complete explanation.
+हमे ज्ञात है कि वृत्त के व्यास के अतिरिक्त किसी जीवा के अंतिम बिंदु उसे दो चापों में विभाजित करते हैं, जिन्हें दीर्घ चाप और लघु चाप कहते हैं। इस लेख में हम वृत्त के चाप द्वारा अंतरित कोण से संबंधित प्रमेय और उसके पूर्ण स्पष्टीकरण के साथ उसके प्रमाण पर चर्चा करेंगे।
-[[File:Equal chords.jpg|alt=Fig. 1|none|thumb|194x194px|Fig. 1]]
-If two chords of a circle are equal, then their corresponding arcs are congruent and conversely, if two arcs are congruent, then their corresponding chords are equal.
-Also the angle subtended by an arc at the centre
+== एक वृत्त के चाप द्वारा अंतरित कोण – प्रमेय एवं प्रमाण ==
+'''प्रमेय:'''
-is defined to be angle subtended by the corresponding
+एक चाप द्वारा केंद्र पर बनाया गया कोण वृत्त के शेष भाग पर किसी भी बिंदु पर बनाए गए कोण का दोगुना होता है।
-chord at the centre in the sense that the minor arc
+'''प्रमाण:'''
-subtends the angle and the major arc subtends the
+केंद्र <math>O</math> वाले एक वृत्त पर विचार करें। यहाँ वृत्त का चाप <math>PQ</math> केंद्र <math>O</math> पर कोण <math>\angle POQ</math> तथा वृत्त के शेष भाग पर स्थित बिंदु <math>A</math> पर कोण <math>\angle PAQ</math> अंतरित करता है।
-reflex angle. Therefore, in Fig 2, the angle
+प्रमाण करने हेतु : <math>\angle POQ = 2 \angle PAQ</math>
-subtended by the minor arc PQ at O is ∠POQ and
+इसे प्रमाणित करने के लिए, <math>AO</math> को जोड़ें और इसे बिंदु <math>B</math> तक विस्तारित करें
-the angle subtended b
+इस प्रमेय को सिद्ध करते समय दो सामान्य स्थितियाँ हैं।
+'''स्थिति 1:'''
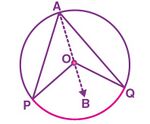
+[[File:Circle-3.jpg|alt=Fig. 1|none|thumb|150x150px|चित्र -1]]
+त्रिभुज <math>APO</math> पर विचार करें
+यहाँ, <math>OA=OP</math> (त्रिज्या)
+चूँकि समान भुजाओं के विपरीत कोण समान होते हैं,
+<math>\angle OPA = \angle OAP .... (1)</math>
+इसके अतिरिक्त, बाह्य कोण गुण (बाह्य कोण आंतरिक विपरीत कोणों का योग है) का उपयोग करते हुए,
+हम लिख सकते हैं,
+<math>\angle BOP = \angle OAP + \angle OPA</math>
+<math>(1)</math> का उपयोग करके
+<math>\angle BOP = \angle OAP + \angle OAP</math>
+<math>\angle BOP = 2 \angle OAP .... (2)</math>
+इसी प्रकार, एक अन्य त्रिभुज <math>AQO</math> पर विचार करें ,
+<math>OA=OQ</math> (त्रिज्या)
+चूँकि समान भुजाओं के विपरीत कोण समान होते हैं,
+<math>\angle OQA = \angle OAQ .... (3)</math>
+इसी प्रकार, बाह्य कोण गुण का उपयोग करके, हम  <math>\angle BOQ = \angle OAQ + \angle OQA</math> प्राप्त करते हैं
+<math>\angle BOQ = \angle OAQ + \angle OAQ</math> (<math>(3)</math>का उपयोग करते हुए)
+<math>\angle BOQ = 2 \angle OAQ .... (4)</math>
+<math>(2)</math> और <math>(4)</math> को जोड़ने पर हमें प्राप्त होता है
+<math>\angle BOP +\angle BOQ =2\angle OAP +2\angle OAQ</math>
+<math>\angle POQ =2(\angle OAP +\angle OAQ)</math>
+<math>\angle POQ =2\angle PAQ</math>
+अतः, स्थिति (1) सिद्ध होती है।
+'''स्थिति 2:'''
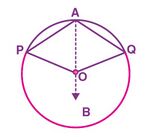
+[[File:Circle-4.jpg|alt=Fig. 2|none|thumb|150x150px|चित्र -2]]
+इस स्थिति में <math>\angle POQ =2\angle PAQ</math> को प्रमाणित करने के लिए, हम स्थिति (1) के समान ही चरणों का पालन कर सकते हैं। लेकिन (2) और (4) को जोड़ते समय हमें नीचे दिए गए चरणों का पालन करना होगा।
+<math>\angle BOP +\angle BOQ =2\angle OAP +2\angle OAQ</math>
+प्रतिवर्ती कोण <math>\angle POQ =2(\angle OAP +\angle OAQ)</math> (चूँकि,<math>PQ</math> एक दीर्घ चाप है)
+प्रतिवर्ती कोण <math>\angle POQ =2\angle PAQ</math>.
+अतः सिद्ध हुआ।
 [[Category:वृत्त]][[Category:कक्षा-9]][[Category:गणित]]