हमे ज्ञात है कि वृत्त के व्यास के अतिरिक्त किसी जीवा के अंतिम बिंदु उसे दो चापों में विभाजित करते हैं, जिन्हें दीर्घ चाप और लघु चाप कहते हैं। इस लेख में हम वृत्त के चाप द्वारा अंतरित कोण से संबंधित प्रमेय और उसके पूर्ण स्पष्टीकरण के साथ उसके प्रमाण पर चर्चा करेंगे।
एक वृत्त के चाप द्वारा अंतरित कोण – प्रमेय एवं प्रमाण
प्रमेय:
एक चाप द्वारा केंद्र पर बनाया गया कोण वृत्त के शेष भाग पर किसी भी बिंदु पर बनाए गए कोण का दोगुना होता है।
प्रमाण:
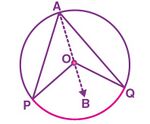
केंद्र  वाले एक वृत्त पर विचार करें। यहाँ वृत्त का चाप
वाले एक वृत्त पर विचार करें। यहाँ वृत्त का चाप  केंद्र
केंद्र  पर कोण
पर कोण  तथा वृत्त के शेष भाग पर स्थित बिंदु
तथा वृत्त के शेष भाग पर स्थित बिंदु  पर कोण
पर कोण  अंतरित करता है।
अंतरित करता है।
प्रमाण करने हेतु : 
इसे प्रमाणित करने के लिए,  को जोड़ें और इसे बिंदु
को जोड़ें और इसे बिंदु  तक विस्तारित करें
तक विस्तारित करें
इस प्रमेय को सिद्ध करते समय दो सामान्य स्थितियाँ हैं।
स्थिति 1:
त्रिभुज  पर विचार करें
पर विचार करें
यहाँ,  (त्रिज्या)
(त्रिज्या)
चूँकि समान भुजाओं के विपरीत कोण समान होते हैं,

इसके अतिरिक्त, बाह्य कोण गुण (बाह्य कोण आंतरिक विपरीत कोणों का योग है) का उपयोग करते हुए,
हम लिख सकते हैं,

 का उपयोग करके
का उपयोग करके


इसी प्रकार, एक अन्य त्रिभुज  पर विचार करें ,
पर विचार करें ,
 (त्रिज्या)
(त्रिज्या)
चूँकि समान भुजाओं के विपरीत कोण समान होते हैं,

इसी प्रकार, बाह्य कोण गुण का उपयोग करके, हम  प्राप्त करते हैं
प्राप्त करते हैं
 (
( का उपयोग करते हुए)
का उपयोग करते हुए)

 और
और  को जोड़ने पर हमें प्राप्त होता है
को जोड़ने पर हमें प्राप्त होता है



अतः, स्थिति (1) सिद्ध होती है।
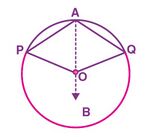
स्थिति 2:
इस स्थिति में  को प्रमाणित करने के लिए, हम स्थिति (1) के समान ही चरणों का पालन कर सकते हैं। लेकिन (2) और (4) को जोड़ते समय हमें नीचे दिए गए चरणों का पालन करना होगा।
को प्रमाणित करने के लिए, हम स्थिति (1) के समान ही चरणों का पालन कर सकते हैं। लेकिन (2) और (4) को जोड़ते समय हमें नीचे दिए गए चरणों का पालन करना होगा।

प्रतिवर्ती कोण  (चूँकि,
(चूँकि, एक दीर्घ चाप है)
एक दीर्घ चाप है)
प्रतिवर्ती कोण  .
.
अतः सिद्ध हुआ।