त्रिकोणमिति: Difference between revisions
(ad) |
(image added) |
||
| Line 16: | Line 16: | ||
समकोण त्रिभुज में निम्नलिखित तीन भुजाएँ होती हैं। | समकोण त्रिभुज में निम्नलिखित तीन भुजाएँ होती हैं। | ||
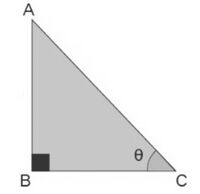
[[File:Right angled triangle.jpg|alt=Fig. 1|none|thumb|200x200px| | [[File:Right angled triangle.jpg|alt=Fig. 1|none|thumb|200x200px|चित्र. 1]] | ||
लम्बवत - यह कोण <math>\theta</math> के सम्मुख भुजा है। | लम्बवत - यह कोण <math>\theta</math> के सम्मुख भुजा है। | ||
Latest revision as of 08:08, 4 November 2024
त्रिकोणमिति
त्रिकोणमिति गणित की वह शाखा है जो समकोण त्रिभुज की भुजाओं के अनुपात और उसके कोणों के बीच के संबंध से संबंधित है। यह ग्रीक शब्द ‘त्रि’ से लिया गया है, जिसका अर्थ है तीन, ‘गॉन’ जिसका अर्थ है भुजाएं, ‘मेट्रोन’ का अर्थ है माप। इसका उपयोग आरंभ के खगोलविदों और मिस्र और बेबीलोन में किया गया था। इस इकाई में हम त्रिकोणमिति क्या है यह जानेंगे ।इस संबंध का अध्ययन करने के लिए उपयोग किए जाने वाले अनुपात को त्रिकोणमितीय अनुपात कहा जाता है, अर्थात्, साइन, कोसाइन, स्पर्शरेखा, कोटैंजेंट, सेकेंट, कोसेकेंट। त्रिकोणमिति शब्द 16वीं शताब्दी का लैटिन व्युत्पन्न है और यह अवधारणा ग्रीक गणितज्ञ हिप्पार्कस द्वारा दी गई थी।
त्रिकोणमिति की खोज
त्रिकोणमिति का आविष्कार और प्रयोग प्राचीन भारत में किया गया। त्रिकोणमिति के जनक, शून्य और दशमलव का महत्व बताने वाले विश्व के महान गणितज्ञ और खगोलशास्त्री आर्यभट् हैं।
त्रिकोणमिति का परिचय
त्रिकोणमिति गणित की सबसे महत्वपूर्ण शाखाओं में से एक है। त्रिकोणमिति गणित की वह शाखा है, जिसमें त्रिभुज की तीनों भुजाओं और तीनों कोणों का अध्ययन किया जाता है।त्रिकोणमिति का अर्थ त्रिभुज की तीनों भुजाओं का माप होता है।
त्रिकोणमिति शब्द 'ट्रिगोनन' और 'मेट्रोन' शब्दों को मिलाकर बनाया गया है, जिसका अर्थ क्रमशः त्रिभुज और माप है। यह समकोण त्रिभुज की भुजाओं और कोणों के बीच के संबंध का अध्ययन है। इस प्रकार यह इस संबंध पर आधारित सूत्रों और सर्वसमिकाओं का उपयोग करके एक समकोण त्रिभुज के अज्ञात आयामों का माप खोजने में मदद करता है।
विभिन्न कोणों (0 से 90 डिग्री(घात)) के लिए त्रिकोणमिति और त्रिकोणमितीय अनुपातों का प्रयोग करने के बाद इसका उपयोग आर्किटेक्चर, इंजीनियरिंग, भौतिक विज्ञान जैसे विषय में देख सकते हैं।
त्रिकोणमिति के मूल तत्व
त्रिकोणमिति की मूल बातें कोणों की माप और कोणों से संबंधित समस्याओं से संबंधित हैं। त्रिकोणमिति में तीन मूल फलन हैं: साइन, कोसाइन और स्पर्शरेखा। इन तीन मूल अनुपातों या फलनों का उपयोग अन्य महत्वपूर्ण त्रिकोणमितीय फलन प्राप्त करने के लिए किया जा सकता है: कोटैंजेंट, सेकेंट और कोसेकेंट। त्रिकोणमिति के अंतर्गत आने वाली सभी महत्वपूर्ण अवधारणाएँ इन फलनों पर आधारित हैं। इसलिए, आगे, हमें त्रिकोणमिति को समझने के लिए पहले इन फलनों और उनके संबंधित सूत्रों को सीखने की आवश्यकता है।
समकोण त्रिभुज में निम्नलिखित तीन भुजाएँ होती हैं।
लम्बवत - यह कोण के सम्मुख भुजा है।
आधार - यह कोण की आसन्न भुजा है।
कर्ण - यह समकोण के सम्मुख भुजा है।
त्रिकोणमितीय अनुपात
त्रिकोणमिति में मूल छह अनुपात होते हैं जो एक समकोण त्रिभुज की भुजाओं के अनुपात और कोण के बीच संबंध स्थापित करने में सहायता करते हैं। यदि समकोण त्रिभुज में आधार और कर्ण के बीच बना कोण है, तो
- = लंबवत/कर्ण
- =आधार/कर्ण
- = लंबवत/आधार
अन्य तीन फलनों का मान क्रमशः नीचे दिए गए अनुसार निर्भर है
- =आधार/लंबवत
- = कर्ण/आधार
- = कर्ण/लंबवत
त्रिकोणमिति का उपयोग
त्रिकोणमिति का उपयोग गणित, विज्ञान और तकनीकी में किया जाता है। त्रिकोणमिति के अध्ययन के बाद हम इसका उपयोग निम्न चीजों में देखते हैं-
- खेतों, भूखंडों और क्षेत्रों को मापना
- सिरेमिक टाइल की माप