सांतत्य: Difference between revisions
(formulas) |
(image added) |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== किसी फलन का सांतत्य == | == किसी फलन का सांतत्य == | ||
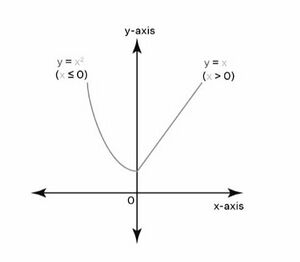
आलेख <math>y = f(x)</math> के लिए सांतत्य को सरलता से संतत के रूप में परिभाषित किया जा सकता है यदि हम किसी बिंदु पर पेंसिल उठाए बिना आसानी से आलेख खींचने में सक्षम हैं। मान लें कि <math>f(x)</math> [[वास्तविक संख्याओं पर संक्रियाएँ|वास्तविक संख्याओं]] के उपसमुच्चय पर एक वास्तविक-मूल्यवान फलन है और <math>c</math> फलन <math>f(x)</math> के | [[File:सांतत्य-फलन x=0 पर सतत है.jpg|thumb|सांतत्य-फलन x=0 पर सतत है]] | ||
आलेख <math>y = f(x)</math> के लिए सांतत्य को सरलता से संतत के रूप में परिभाषित किया जा सकता है यदि हम किसी बिंदु पर पेंसिल उठाए बिना आसानी से आलेख खींचने में सक्षम हैं। मान लें कि <math>f(x)</math> [[वास्तविक संख्याओं पर संक्रियाएँ|वास्तविक संख्याओं]] के उपसमुच्चय पर एक वास्तविक-मूल्यवान फलन है और <math>c</math> फलन <math>f(x)</math> के प्रांत में उपस्थित एक बिंदु है। तब हम कहते हैं कि फलन <math>f(x)</math> बिंदु <math>x = c</math> पर संतत है यदि हमारे पास <math>\textstyle \lim_{x \to c} \displaystyle f (x)=f(c)</math> है। | |||
किसी [[फलन]] की सांतत्य को आलेखीय रूप से या बीजगणितीय रूप से समझाया जा सकता है। आलेख में बिंदु पर फलन <math>y = f(x)</math> की सांतत्य एक आलेख रेखा है जो बिना किसी रुकावट के बिंदु से लगातार गुजरती है। फलन <math>y = f(x)</math> की सांतत्य को बीजगणितीय रूप से देखा जा सकता है यदि फलन का मान बाएं हाथ की सीमा से फलन के मान के बराबर है। <math> \textstyle \lim_{x \to 1^{-1}} \displaystyle f(x)=\textstyle \lim_{x \to 1^{+1}} \displaystyle f(x)</math>। यानी <math>x = 0.99, 0.998</math> के मान, जो <math>1</math> से थोड़े कम हैं, का <math>f(x)</math> फलन मान <math>x = 1.001, 1.0001</math> के समान है, जो <math>1</math> से थोड़े अधिक हैं। | |||
== सांतत्य और अवकलनीयता पर प्रमेय == | == सांतत्य और अवकलनीयता पर प्रमेय == | ||
सांतत्य और अवकलनीयता पर निम्नलिखित महत्वपूर्ण प्रमेय, सांतत्य और अवकलनीयता की अवधारणाओं की गहन समझ के लिए सही पृष्ठभूमि निर्धारित करते हैं। | सांतत्य और [[अवकलनीयता]] पर निम्नलिखित महत्वपूर्ण प्रमेय, सांतत्य और अवकलनीयता की अवधारणाओं की गहन समझ के लिए सही पृष्ठभूमि निर्धारित करते हैं। | ||
=== प्रमेय 1: === | === प्रमेय 1: === | ||
| Line 22: | Line 19: | ||
=== प्रमेय 2: === | === प्रमेय 2: === | ||
दो वास्तविक मान फलन <math>f(x)</math> और <math>g(x)</math> के लिए जैसे कि समग्र फलन <math>fog(x)</math>, <math> x = c</math> पर परिभाषित किया गया है। यदि <math>g(x), x = c</math>पर सतत है और फलन <math>f(x), g(c)</math>पर सतत है, तो<math>fog(x)</math>, <math> x = c</math> पर सतत है। | दो वास्तविक मान फलन <math>f(x)</math> और <math>g(x)</math> के लिए जैसे कि समग्र फलन <math>fog(x)</math>, <math> x = c</math> पर परिभाषित किया गया है। यदि <math>g(x), x = c</math> पर सतत है और फलन <math>f(x), g(c)</math>पर सतत है, तो<math>fog(x)</math>, <math> x = c</math> पर सतत है। | ||
=== प्रमेय 3: === | === प्रमेय 3: === | ||
| Line 28: | Line 25: | ||
=== प्रमेय 4: === | === प्रमेय 4: === | ||
श्रृंखला नियम: एक वास्तविक मान वाले फलन <math>f(x)</math> के लिए, जो दो फलन <math>u</math> और <math>v</math> का संयोजन है, अर्थात,<math>f = vou</math>। साथ ही मान लें कि <math>t = u(x)</math> है और यदि <math> {dt \over dx}</math>और <math> {dv \over dt}</math> दोनों उपस्थित हैं, तो हमारे पास <math> {df \over dx} = {dv \over dt}\cdot dt\cdot dx</math> है। | '''श्रृंखला नियम''': एक वास्तविक मान वाले फलन <math>f(x)</math> के लिए, जो दो फलन <math>u</math> और <math>v</math> का संयोजन है, अर्थात,<math>f = vou</math>। साथ ही मान लें कि <math>t = u(x)</math> है और यदि <math> {dt \over dx}</math>और <math> {dv \over dt}</math> दोनों उपस्थित हैं, तो हमारे पास <math> {df \over dx} = {dv \over dt}\cdot dt\cdot dx</math> है। | ||
=== प्रमेय 5: === | === प्रमेय 5: === | ||
Latest revision as of 13:43, 30 November 2024
किसी फलन का सांतत्य
आलेख के लिए सांतत्य को सरलता से संतत के रूप में परिभाषित किया जा सकता है यदि हम किसी बिंदु पर पेंसिल उठाए बिना आसानी से आलेख खींचने में सक्षम हैं। मान लें कि वास्तविक संख्याओं के उपसमुच्चय पर एक वास्तविक-मूल्यवान फलन है और फलन के प्रांत में उपस्थित एक बिंदु है। तब हम कहते हैं कि फलन बिंदु पर संतत है यदि हमारे पास है।
किसी फलन की सांतत्य को आलेखीय रूप से या बीजगणितीय रूप से समझाया जा सकता है। आलेख में बिंदु पर फलन की सांतत्य एक आलेख रेखा है जो बिना किसी रुकावट के बिंदु से लगातार गुजरती है। फलन की सांतत्य को बीजगणितीय रूप से देखा जा सकता है यदि फलन का मान बाएं हाथ की सीमा से फलन के मान के बराबर है। । यानी के मान, जो से थोड़े कम हैं, का फलन मान के समान है, जो से थोड़े अधिक हैं।
सांतत्य और अवकलनीयता पर प्रमेय
सांतत्य और अवकलनीयता पर निम्नलिखित महत्वपूर्ण प्रमेय, सांतत्य और अवकलनीयता की अवधारणाओं की गहन समझ के लिए सही पृष्ठभूमि निर्धारित करते हैं।
प्रमेय 1:
यदि दो फलन और एक वास्तविक मान फलन पर संतत हैं और एक बिंदु पर संतत हैं, तो हमारे पास है:
बिंदु पर संतत है
एक बिंदु पर संतत है
बिंदु पर संतत है
एक बिंदु पर संतत है, बशर्ते
प्रमेय 2:
दो वास्तविक मान फलन और के लिए जैसे कि समग्र फलन , पर परिभाषित किया गया है। यदि पर सतत है और फलन पर सतत है, तो, पर सतत है।
प्रमेय 3:
यदि दिया गया फलन किसी बिंदु पर अवकलनीय है, तो वह उस बिंदु पर सतत है। इसे संक्षेप में इस प्रकार कहा जा सकता है कि प्रत्येक अवकलनीय फलन सतत है।
प्रमेय 4:
श्रृंखला नियम: एक वास्तविक मान वाले फलन के लिए, जो दो फलन और का संयोजन है, अर्थात,। साथ ही मान लें कि है और यदि और दोनों उपस्थित हैं, तो हमारे पास है।
प्रमेय 5:
के सापेक्ष का अवकलज है। और के सापेक्ष का अवकलज है।
प्रमेय 6:
(रोले का प्रमेय)। यदि कोई फलन अंतराल में संतत है और अंतराल में अवकलनीय है, जैसे कि और कुछ वास्तविक संख्याएँ हैं। तब अंतरालमें एक बिंदु उपस्थित होता है जैसे कि
प्रमेय 7:
(माध्य मान प्रमेय)। यदि कोई फलन अंतराल में संतत है और अंतराल में अवकलनीय है, तो अंतराल में एक बिंदु उपस्थित होता है जैसे कि