एक ही रेखा के समानांतर रेखाएँ: Difference between revisions
From Vidyalayawiki
(added content) |
(added content) |
||
| Line 8: | Line 8: | ||
हम जानते हैं कि रेखा <math>m || </math> रेखा <math>l </math> और रेखा <math>n || </math> रेखा <math>l </math> है। | हम जानते हैं कि रेखा <math>m || </math> रेखा <math>l </math> और रेखा <math>n || </math> रेखा <math>l </math> है। | ||
अतः <math>\angle 1=\angle 2 </math> और <math>\angle 1=\angle 3 </math> (संगत कोण अभिगृहीत) | |||
परंतु <math>\angle 2=\angle 3 </math> क्योंकि वे संगत कोण हैं | |||
अतः, हम कह सकते हैं कि रेखा <math>m || </math> रेखा <math>n </math> (संगत कोण अभिगृहीत का विलोम) | |||
इस परिणाम को निम्नलिखित प्रमेय के रूप में बताया जा सकता है: | |||
'''प्रमेय 1:''' वे रेखाएँ जो एक ही रेखा के समानान्तर होती हैं, एक दूसरे के समानान्तर होती हैं। | |||
[[Category:रेखाएँ और कोण]][[Category:कक्षा-9]][[Category:गणित]] | [[Category:रेखाएँ और कोण]][[Category:कक्षा-9]][[Category:गणित]] | ||
Revision as of 08:23, 1 July 2024
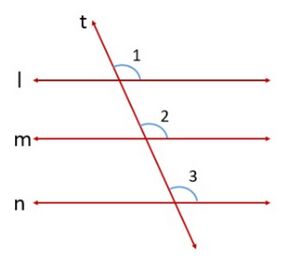
यदि दो रेखाएँ एक ही रेखा के समानान्तर हों तो क्या वे एक-दूसरे के समानान्तर होंगी? आइए सत्यापित करें।
चित्र-1 में रेखा रेखा और रेखा रेखा ।
आइए हम रेखाओं के लिए एक रेखा अनुप्रस्थ रेखा खींचें
हम जानते हैं कि रेखा रेखा और रेखा रेखा है।
अतः और (संगत कोण अभिगृहीत)
परंतु क्योंकि वे संगत कोण हैं
अतः, हम कह सकते हैं कि रेखा रेखा (संगत कोण अभिगृहीत का विलोम)
इस परिणाम को निम्नलिखित प्रमेय के रूप में बताया जा सकता है:
प्रमेय 1: वे रेखाएँ जो एक ही रेखा के समानान्तर होती हैं, एक दूसरे के समानान्तर होती हैं।