एक वृत्त के चाप द्वारा अंतरित कोण: Difference between revisions
(added content) |
No edit summary |
||
| Line 1: | Line 1: | ||
We know that the end points of a chord other than the diameter of a circle divides it into two arcs, namely the major arc and the minor arc. In this article, we will discuss the theorem related to the angle subtended by an arc of a circle and its proof with complete explanation. | |||
== Angle Subtended by an Arc of a Circle – Theorem and Proof == | |||
=== Theorem: === | |||
The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle. | |||
'''Proof:''' | |||
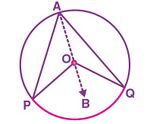
Consider a circle with centre <math>O</math>. Here the arc <math>PQ</math> of the circle subtends angle <math>\angle POQ</math> at Centre <math>O</math> and <math>\angle PAQ</math> at a point <math>A</math> on the remaining part of the circle. | |||
To prove: <math>\angle POQ = 2 \angle PAQ</math> | |||
To prove this, join <math>AO</math> and extend it to point <math>B</math>. | |||
There are two general cases while proving this theorem. | |||
'''Case 1:''' | |||
[[File:Circle-3.jpg|alt=Fig. 1|none|thumb|150x150px|Fig. 1]] | |||
Consider a triangle <math>APO</math> | |||
Here, <math>OA=OP</math> (Radii) | |||
Since, the angles opposite to the equal sides are equal, | |||
<math>\angle OPA = \angle OAP .... (1)</math> | |||
Also, by using the exterior angle property (exterior angle is the sum of interior opposite angles), | |||
We can write, | |||
<math>\angle BOP = \angle OAP + \angle OPA</math> | |||
By using <math>(1)</math> | |||
<math>\angle BOP = \angle OAP + \angle OAP</math> | |||
<math>\angle BOP = 2 \angle OAP .... (2)</math> | |||
Similarly, consider another triangle <math>AQO</math>, | |||
<math>OA=OQ</math> (Radii) | |||
As the angles opposite to the equal sides are equal, | |||
<math>\angle OQA = \angle OAQ .... (3)</math> | |||
Similarly, by using the exterior angle property, we get<math>\angle BOQ = \angle OAQ + \angle OQA</math> | |||
<math>\angle BOQ = \angle OAQ + \angle OAQ</math> (using <math>(3)</math>) | |||
<math>\angle BOQ = 2 \angle OAQ .... (4)</math> | |||
Adding <math>(2)</math>and <math>(4)</math> we get, | |||
<math>\angle BOP +\angle BOQ =2\angle OAP +2\angle OAQ</math> | |||
<math>\angle POQ =2(\angle OAP +\angle OAQ)</math> | |||
<math>\angle POQ =2\angle PAQ</math> | |||
Hence, case (1) is proved. | |||
'''Case 2:''' | |||
[[File:Circle-4.jpg|alt=Fig. 2|none|thumb|150x150px|Fig. 2]] | |||
To prove <math>\angle POQ =2\angle PAQ</math> for this case, we can follow the steps as same as for case <math>(1)</math>. But while adding <math>(2)</math> and<math>(4)</math>, we have to follow the below steps. | |||
<math>\angle BOP +\angle BOQ =2\angle OAP +2\angle OAQ</math> | |||
Reflex angle <math>\angle POQ =2(\angle OAP +\angle OAQ)</math> (Since, <math>PQ</math> is a Major arc) | |||
Reflex angle <math>\angle POQ =2\angle PAQ</math>. | |||
Hence, proved. | |||
[[Category:वृत्त]][[Category:कक्षा-9]][[Category:गणित]] | [[Category:वृत्त]][[Category:कक्षा-9]][[Category:गणित]] | ||
Revision as of 17:55, 17 September 2024
We know that the end points of a chord other than the diameter of a circle divides it into two arcs, namely the major arc and the minor arc. In this article, we will discuss the theorem related to the angle subtended by an arc of a circle and its proof with complete explanation.
Angle Subtended by an Arc of a Circle – Theorem and Proof
Theorem:
The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
Proof:
Consider a circle with centre . Here the arc of the circle subtends angle at Centre and at a point on the remaining part of the circle.
To prove:
To prove this, join and extend it to point .
There are two general cases while proving this theorem.
Case 1:
Consider a triangle
Here, (Radii)
Since, the angles opposite to the equal sides are equal,
Also, by using the exterior angle property (exterior angle is the sum of interior opposite angles),
We can write,
By using
Similarly, consider another triangle ,
(Radii)
As the angles opposite to the equal sides are equal,
Similarly, by using the exterior angle property, we get
(using )
Adding and we get,
Hence, case (1) is proved.
Case 2:
To prove for this case, we can follow the steps as same as for case . But while adding and, we have to follow the below steps.
Reflex angle (Since, is a Major arc)
Reflex angle .
Hence, proved.