एक वृत्त के चाप द्वारा अंतरित कोण: Difference between revisions
No edit summary |
(added content) |
||
| Line 1: | Line 1: | ||
हमे ज्ञात है कि वृत्त के व्यास के अतिरिक्त किसी जीवा के अंतिम बिंदु उसे दो चापों में विभाजित करते हैं, जिन्हें दीर्घ चाप और लघु चाप कहते हैं। इस लेख में हम वृत्त के चाप द्वारा अंतरित कोण से संबंधित प्रमेय और उसके पूर्ण स्पष्टीकरण के साथ उसके प्रमाण पर चर्चा करेंगे। | |||
== | == एक वृत्त के चाप द्वारा अंतरित कोण – प्रमेय एवं प्रमाण == | ||
'''प्रमेय:''' | |||
एक चाप द्वारा केंद्र पर बनाया गया कोण वृत्त के शेष भाग पर किसी भी बिंदु पर बनाए गए कोण का दोगुना होता है। | |||
''' | '''प्रमाण:''' | ||
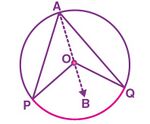
केंद्र <math>O</math> वाले एक वृत्त पर विचार करें। यहाँ वृत्त का चाप <math>PQ</math> केंद्र <math>O</math> पर कोण <math>\angle POQ</math> तथा वृत्त के शेष भाग पर स्थित बिंदु <math>A</math> पर कोण <math>\angle PAQ</math> अंतरित करता है। | |||
प्रमाण करने हेतु : <math>\angle POQ = 2 \angle PAQ</math> | |||
इसे प्रमाणित करने के लिए, <math>AO</math> को जोड़ें और इसे बिंदु <math>B</math> तक विस्तारित करें | |||
इस प्रमेय को सिद्ध करते समय दो सामान्य स्थितियाँ हैं। | |||
''' | '''स्थिति 1:''' | ||
[[File:Circle-3.jpg|alt=Fig. 1|none|thumb|150x150px| | [[File:Circle-3.jpg|alt=Fig. 1|none|thumb|150x150px|चित्र -1]] | ||
Consider a triangle <math>APO</math> | Consider a triangle <math>APO</math> | ||
Revision as of 18:10, 17 September 2024
हमे ज्ञात है कि वृत्त के व्यास के अतिरिक्त किसी जीवा के अंतिम बिंदु उसे दो चापों में विभाजित करते हैं, जिन्हें दीर्घ चाप और लघु चाप कहते हैं। इस लेख में हम वृत्त के चाप द्वारा अंतरित कोण से संबंधित प्रमेय और उसके पूर्ण स्पष्टीकरण के साथ उसके प्रमाण पर चर्चा करेंगे।
एक वृत्त के चाप द्वारा अंतरित कोण – प्रमेय एवं प्रमाण
प्रमेय:
एक चाप द्वारा केंद्र पर बनाया गया कोण वृत्त के शेष भाग पर किसी भी बिंदु पर बनाए गए कोण का दोगुना होता है।
प्रमाण:
केंद्र वाले एक वृत्त पर विचार करें। यहाँ वृत्त का चाप केंद्र पर कोण तथा वृत्त के शेष भाग पर स्थित बिंदु पर कोण अंतरित करता है।
प्रमाण करने हेतु :
इसे प्रमाणित करने के लिए, को जोड़ें और इसे बिंदु तक विस्तारित करें
इस प्रमेय को सिद्ध करते समय दो सामान्य स्थितियाँ हैं।
स्थिति 1:
Consider a triangle
Here, (Radii)
Since, the angles opposite to the equal sides are equal,
Also, by using the exterior angle property (exterior angle is the sum of interior opposite angles),
We can write,
By using
Similarly, consider another triangle ,
(Radii)
As the angles opposite to the equal sides are equal,
Similarly, by using the exterior angle property, we get
(using )
Adding and we get,
Hence, case (1) is proved.
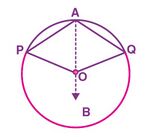
Case 2:
To prove for this case, we can follow the steps as same as for case . But while adding and, we have to follow the below steps.
Reflex angle (Since, is a Major arc)
Reflex angle .
Hence, proved.