समान जीवाएं और उनकी केंद्र से दूरीयाँ: Difference between revisions

Latest revision as of 16:46, 18 September 2024

जीवा एक रेखाखंड है जो वृत्त की परिधि पर दो बिंदुओं को जोड़ता है। सामान्यतः, एक वृत्त में अनंत जीवाएँ हो सकती हैं। एक बिंदु से रेखा की दूरी को एक बिंदु से एक रेखा तक लंबवत दूरी के रूप में परिभाषित किया जाता है। यदि हम एक वृत्त पर अनंत जीवाएँ खींचते हैं, तो लंबी जीवा वृत्त के केंद्र के करीब होती है, छोटी जीवा की तुलना में। यहां हम समान जीवाओं और केंद्र से उनकी दूरी से संबंधित प्रमेय और प्रमाण तथा इसके व्युत्क्रम प्रमेय पर विस्तार से चर्चा करेंगे।

समान जीवाएं और उनकी केंद्र से दूरीयाँ – प्रमेय एवं प्रमाण

प्रमेय :

एक वृत्त (या सर्वांगसम वृत्तों) की समान जीवाएँ केंद्र (या केंद्रों) से समान दूरी पर होती हैं।

प्रमाण:

चित्र -2

केंद्र $O$ वाले एक वृत्त पर विचार करें।

$AB$ और $CD$ एक वृत्त की समान जीवाएँ हैं अर्थात् $AB=CD$

रेखा $OX$ जीवा $AB$ पर लंबवत है और $OY$ जीवा $CD$ पर लंबवत है।

हमें प्रमाणित करना होगा $OX=OY$ .

साथ ही, रेखा $OX$ , $AB$ पर लंबवत है।

चूँकि वृत्त के केंद्र से जीवा पर डाला गया लंब जीवा को समद्विभाजित करता है, इसलिए हम इसे इस प्रकार लिख सकते हैं

$AX=BX={\frac {AB}{2}}....(1)$

इसी प्रकार, रेखा $OY$ , $CD$ पर लंबवत है,

$CY=DY={\frac {CD}{2}}....(2)$ [चूँकि वृत्त के केंद्र से जीवा पर डाला गया लंब, जीवा को समद्विभाजित करता है)

मान लें कि, $AB=CD$

${\frac {AB}{2}}={\frac {CD}{2}}....(2)$

अत:, $AX=CY....(3)$ [ $(1)$ और $(2)$ का उपयोग करते हुए]

अब, त्रिभुजों का उपयोग करके $AOX$ और $COY$ ,

$\angle OXA=\angle OYC=90^{\circ }$

$OA=OC$ (त्रिज्या)

$AX=CY....(3)$

RHS नियम से, हम इसे इस प्रकार लिख सकते हैं

$\triangle AOX\cong \triangle COY$

अतः हम यह निष्कर्ष निकाल सकते हैं कि $OX=OY$ (CPCT का उपयोग करते हुए)

इसलिए, प्रमेय "एक वृत्त (या सर्वांगसम वृत्तों) की समान जीवाएँ केंद्र (या केंद्रों) से समान दूरी पर होती हैं", सिद्ध होता है।

इस प्रमेय का व्युत्क्रम:

उपर्युक्त प्रमेय का व्युत्क्रम है "वृत्त के केंद्र से समान दूरी पर स्थित जीवाएँ लंबाई में समान होती हैं"।

@@ Line 1: / Line 1: @@
 जीवा एक रेखाखंड है जो वृत्त की परिधि पर दो बिंदुओं को जोड़ता है। सामान्यतः, एक वृत्त में अनंत जीवाएँ हो सकती हैं। एक बिंदु से रेखा की दूरी को एक बिंदु से एक रेखा तक लंबवत दूरी के रूप में परिभाषित किया जाता है। यदि हम एक वृत्त पर अनंत जीवाएँ खींचते हैं, तो लंबी जीवा वृत्त के केंद्र के करीब होती है, छोटी जीवा की तुलना में। यहां हम समान जीवाओं और केंद्र से उनकी दूरी से संबंधित प्रमेय और प्रमाण तथा इसके व्युत्क्रम प्रमेय पर विस्तार से चर्चा करेंगे।
-== Equal Chords and their Distance from the Centre – Theorem and Proof ==
+== समान जीवाएं और उनकी केंद्र से दूरीयाँ –  प्रमेय एवं प्रमाण ==
-=== Theorem: ===
+=== प्रमेय : ===
-Equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres).
+एक वृत्त (या सर्वांगसम वृत्तों) की समान जीवाएँ केंद्र (या केंद्रों) से समान दूरी पर होती हैं।
-'''Proof:'''
+'''प्रमाण:'''
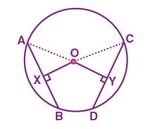
-[[File:Circle-2.jpg|alt=Fig. 2|thumb|150x150px|Fig. 2]]
+[[File:Circle-2.jpg|alt=Fig. 2|thumb|150x150px|चित्र -2]]
-Consider a circle with centre <math>O</math>.
+केंद्र <math>O</math> वाले एक वृत्त पर विचार करें।
-<math>AB</math> and <math>CD</math> are the equal chords of a circle i.e <math>AB=CD</math>
+<math>AB</math> और <math>CD</math> एक वृत्त की समान जीवाएँ हैं अर्थात् <math>AB=CD</math>
-The line <math>OX</math> is perpendicular to the chord <math>AB</math> and <math>OY</math> is perpendicular to the chord <math>CD</math>.
+रेखा <math>OX</math> जीवा <math>AB</math>  पर लंबवत है और <math>OY</math> जीवा <math>CD</math> पर लंबवत है।
-We have to prove <math>OX=OY</math>.
+हमें प्रमाणित करना होगा <math>OX=OY</math>.
-Also, the line <math>OX</math> is perpendicular to <math>AB</math>.
+साथ ही, रेखा <math>OX</math>, <math>AB</math>पर लंबवत है।
-As the perpendicular from the centre of the circle to a chord, bisects the chord, we can write it as
+चूँकि वृत्त के केंद्र से जीवा पर डाला गया लंब जीवा को समद्विभाजित करता है, इसलिए हम इसे इस प्रकार लिख सकते हैं
 <math>AX=BX=\frac{AB}{2} .... (1)</math>
-Similarly, the line <math>OY</math> is perpendicular to <math>CD</math>,
+इसी प्रकार, रेखा <math>OY</math>, <math>CD</math> पर लंबवत है,
-<math>CY=DY=\frac{CD}{2} .... (2)</math> [Since, the perpendicular from the centre of the circle to a chord, bisects the chord)
+<math>CY=DY=\frac{CD}{2} .... (2)</math> [चूँकि वृत्त के केंद्र से जीवा पर डाला गया लंब, जीवा को समद्विभाजित करता है)
-Given that, <math>AB=CD</math>
+मान लें कि, <math>AB=CD</math>
 <math>\frac{AB}{2}=\frac{CD}{2} .... (2)</math>
-Therefore, <math>AX=CY .... (3)</math> [Using <math>(1)</math> and <math>(2)</math>]
+अत:, <math>AX=CY .... (3)</math> [<math>(1)</math> और <math>(2)</math>का उपयोग करते हुए]
-Now, by using the triangles <math>AOX</math> and <math>COY</math> ,
+अब, त्रिभुजों का उपयोग करके <math>AOX</math> और <math>COY</math> ,
 <math>\angle OXA =\angle OYC =90^\circ </math>
-<math>OA =OC </math> (Radii)
+<math>OA =OC </math> (त्रिज्या)
 <math>AX=CY .... (3)</math>
-From the RHS rule, we can write it as
+RHS नियम से, हम इसे इस प्रकार लिख सकते हैं
 <math>\triangle AOX \cong \triangle COY</math>
-Hence, we can conclude that <math>OX=OY</math>(Using CPCT)
+अतः हम यह निष्कर्ष निकाल सकते हैं कि <math>OX=OY</math>(CPCT का उपयोग करते हुए)
-Therefore, the theorem “equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres)”, is proved.
+इसलिए, प्रमेय "एक वृत्त (या सर्वांगसम वृत्तों) की समान जीवाएँ केंद्र (या केंद्रों) से समान दूरी पर होती हैं", सिद्ध होता है।
-=== Converse of this Theorem ===
+=== इस प्रमेय का व्युत्क्रम: ===
-The converse of the above-mentioned theorem is “chords equidistant from the centre of a circle are equal in length”.
+उपर्युक्त प्रमेय का व्युत्क्रम है "वृत्त के केंद्र से समान दूरी पर स्थित जीवाएँ लंबाई में समान होती हैं"।
 [[Category:वृत्त]][[Category:कक्षा-9]][[Category:गणित]]