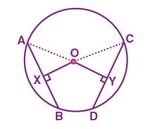
समान जीवाएं और उनकी केंद्र से दूरीयाँ

जीवा एक रेखाखंड है जो वृत्त की परिधि पर दो बिंदुओं को जोड़ता है। सामान्यतः, एक वृत्त में अनंत जीवाएँ हो सकती हैं। एक बिंदु से रेखा की दूरी को एक बिंदु से एक रेखा तक लंबवत दूरी के रूप में परिभाषित किया जाता है। यदि हम एक वृत्त पर अनंत जीवाएँ खींचते हैं, तो लंबी जीवा वृत्त के केंद्र के करीब होती है, छोटी जीवा की तुलना में। यहां हम समान जीवाओं और केंद्र से उनकी दूरी से संबंधित प्रमेय और प्रमाण तथा इसके व्युत्क्रम प्रमेय पर विस्तार से चर्चा करेंगे।

समान जीवाएं और उनकी केंद्र से दूरीयाँ – प्रमेय एवं प्रमाण

प्रमेय :

एक वृत्त (या सर्वांगसम वृत्तों) की समान जीवाएँ केंद्र (या केंद्रों) से समान दूरी पर होती हैं।

प्रमाण:

चित्र -2

केंद्र $O$ वाले एक वृत्त पर विचार करें।

$AB$ और $CD$ एक वृत्त की समान जीवाएँ हैं अर्थात् $AB=CD$

रेखा $OX$ जीवा $AB$ पर लंबवत है और $OY$ जीवा $CD$ पर लंबवत है।

हमें प्रमाणित करना होगा $OX=OY$.

साथ ही, रेखा $OX$, $AB$पर लंबवत है।

चूँकि वृत्त के केंद्र से जीवा पर डाला गया लंब जीवा को समद्विभाजित करता है, इसलिए हम इसे इस प्रकार लिख सकते हैं

$AX=BX={\frac {AB}{2}}....(1)$

इसी प्रकार, रेखा $OY$, $CD$ पर लंबवत है,

$CY=DY={\frac {CD}{2}}....(2)$ [चूँकि वृत्त के केंद्र से जीवा पर डाला गया लंब, जीवा को समद्विभाजित करता है)

मान लें कि, $AB=CD$

${\frac {AB}{2}}={\frac {CD}{2}}....(2)$

अत:, $AX=CY....(3)$ [$(1)$ और $(2)$का उपयोग करते हुए]

अब, त्रिभुजों का उपयोग करके $AOX$ और $COY$ ,

$\angle OXA=\angle OYC=90^{\circ }$

$OA=OC$ (त्रिज्या)

$AX=CY....(3)$

RHS नियम से, हम इसे इस प्रकार लिख सकते हैं

$\triangle AOX\cong \triangle COY$

अतः हम यह निष्कर्ष निकाल सकते हैं कि $OX=OY$(CPCT का उपयोग करते हुए)

इसलिए, प्रमेय "एक वृत्त (या सर्वांगसम वृत्तों) की समान जीवाएँ केंद्र (या केंद्रों) से समान दूरी पर होती हैं", सिद्ध होता है।

इस प्रमेय का व्युत्क्रम:

उपर्युक्त प्रमेय का व्युत्क्रम है "वृत्त के केंद्र से समान दूरी पर स्थित जीवाएँ लंबाई में समान होती हैं"।