एक ही रेखा के समानांतर रेखाएँ: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
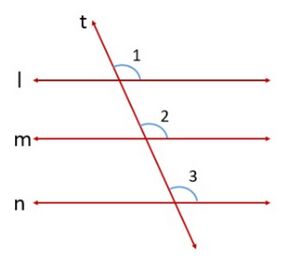
[[File:Transversal Line.jpg|alt=Fig. 1 - Transversal Line|thumb|Fig. 1 - Transversal Line]] | [[File:Transversal Line.jpg|alt=Fig. 1 - Transversal Line|thumb|चित्र -1 अनुप्रस्थ रेखा]] | ||
यदि दो रेखाएँ एक ही रेखा के समानान्तर हों तो क्या वे एक-दूसरे के समानान्तर होंगी? आइए सत्यापित करें। | |||
चित्र-1 में रेखा <math>m || </math> रेखा <math>l </math> और रेखा <math>n || </math> रेखा <math>l </math>। | |||
आइए हम रेखाओं <math>l,m,n </math> के लिए एक रेखा <math>t </math> अनुप्रस्थ रेखा खींचें | |||
हम जानते हैं कि रेखा <math>m || </math> रेखा <math>l </math> और रेखा <math>n || </math> रेखा <math>l </math> है। | |||
अतः <math>\angle 1=\angle 2 </math> और <math>\angle 1=\angle 3 </math> (संगत कोण अभिगृहीत) | |||
परंतु <math>\angle 2=\angle 3 </math> क्योंकि वे संगत कोण हैं | |||
अतः, हम कह सकते हैं कि रेखा <math>m || </math> रेखा <math>n </math> (संगत कोण अभिगृहीत का विलोम) | |||
इस परिणाम को निम्नलिखित प्रमेय के रूप में बताया जा सकता है: | |||
'''प्रमेय 1:''' वे रेखाएँ जो एक ही रेखा के समानान्तर होती हैं, एक दूसरे के समानान्तर होती हैं। | |||
[File:Transversal Line.jpg|alt=Fig. 1 - Transversal Line|thumb|Fig. 1 - Transversal Line]] | |||
If two lines are parallel to the same line, will they be parallel to each other? Let us verify. | If two lines are parallel to the same line, will they be parallel to each other? Let us verify. | ||
| Line 45: | Line 73: | ||
[ | [[[Category:रेखाएँ और कोण]][[Category:कक्षा-9]][[Category:गणित]] | ||
[[Category:रेखाएँ और कोण]][[Category:कक्षा-9]][[Category:गणित]] | |||
Revision as of 12:13, 3 November 2024
यदि दो रेखाएँ एक ही रेखा के समानान्तर हों तो क्या वे एक-दूसरे के समानान्तर होंगी? आइए सत्यापित करें।
चित्र-1 में रेखा रेखा और रेखा रेखा ।
आइए हम रेखाओं के लिए एक रेखा अनुप्रस्थ रेखा खींचें
हम जानते हैं कि रेखा रेखा और रेखा रेखा है।
अतः और (संगत कोण अभिगृहीत)
परंतु क्योंकि वे संगत कोण हैं
अतः, हम कह सकते हैं कि रेखा रेखा (संगत कोण अभिगृहीत का विलोम)
इस परिणाम को निम्नलिखित प्रमेय के रूप में बताया जा सकता है:
प्रमेय 1: वे रेखाएँ जो एक ही रेखा के समानान्तर होती हैं, एक दूसरे के समानान्तर होती हैं।
[File:Transversal Line.jpg|alt=Fig. 1 - Transversal Line|thumb|Fig. 1 - Transversal Line]]
If two lines are parallel to the same line, will they be parallel to each other? Let us verify.
In the fig.1 line line and line line .
Let us draw a line transversal for the lines
We know that line line and line line .
Hence and (Corresponding angles axiom)
But as they are corresponding angles
Therefore, we can say that line line (Converse of corresponding angles axiom)
This result can be stated in the form of the following theorem:
Theorem 1: Lines which are parallel to the same line are parallel to each other.
Example
From the given figure, , , and . Find the values of .
Solution:
Given that , , and
Therefore, (Interior angles on the same side of transversal )
Hence,
By using the corresponding angles axiom, , we can say that .
Therefore, the value of
Since, and , therefore .
So, we can write: (Interior angles on the same side of transversal )
Therefore, the values of are respectively.
[[[Category:रेखाएँ और कोण]]