त्रिकोणमितीय अनुपात: Difference between revisions
(added content) |
(added internal links) |
||
| Line 1: | Line 1: | ||
== परिचय == | == परिचय == | ||
किसी समकोण त्रिभुज में किन्हीं दो भुजाओं के अनुपात को त्रिकोणमितीय अनुपात या त्रिकोणमितीय अनुपात कहते हैं। समकोण त्रिभुज में न्यून कोण का त्रिकोणमितीय अनुपात उसकी भुजाओं के कोण और लंबाई के बीच संबंध को व्यक्त करता है।[[File:Trigonometric ratios -2.jpg|alt=Trigonometric ratio|thumb|त्रिकोणमितीय अनुपात -1. ]] | किसी समकोण त्रिभुज में किन्हीं दो भुजाओं के अनुपात को [[त्रिकोणमिति|त्रिकोणमितीय]] अनुपात या त्रिकोणमितीय अनुपात कहते हैं। समकोण त्रिभुज में न्यून कोण का त्रिकोणमितीय अनुपात उसकी भुजाओं के कोण और लंबाई के बीच संबंध को व्यक्त करता है।[[File:Trigonometric ratios -2.jpg|alt=Trigonometric ratio|thumb|त्रिकोणमितीय अनुपात -1. ]] | ||
[[Category:त्रिकोणमिति का परिचय]] | [[Category:त्रिकोणमिति का परिचय]] | ||
== परिभाषा == | == परिभाषा == | ||
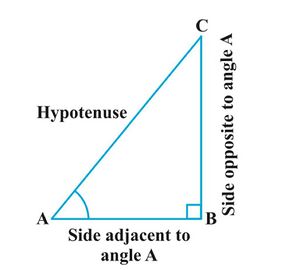
चित्र 1 में दिखाए गए समकोण त्रिभुज <math>\triangle ABC</math> पर विचार करें। यहाँ कोण <math>A</math>(कोण <math>\angle CAB</math>) एक न्यूनकोण है। भुजा <math>BC</math> कोण <math>A</math> के सम्मुख है। इसलिए <math>BC</math> कोण <math>\angle A</math> के विपरीत भुजा है। <math>AC</math> समकोण त्रिभुज <math>\triangle ABC</math> का कर्ण है और भुजा <math>AB</math> कोण <math>\angle A</math> का भाग है। इसलिए <math>AB</math> कोण <math>\angle A</math> से सटी हुई भुजा है। | चित्र 1 में दिखाए गए समकोण त्रिभुज <math>\triangle ABC</math> पर विचार करें। यहाँ कोण <math>A</math>(कोण <math>\angle CAB</math>) एक न्यूनकोण है। भुजा <math>BC</math> कोण <math>A</math> के सम्मुख है। इसलिए <math>BC</math> कोण <math>\angle A</math> के विपरीत भुजा है। <math>AC</math> समकोण [[त्रिभुज]] <math>\triangle ABC</math> का कर्ण है और भुजा <math>AB</math> कोण <math>\angle A</math> का भाग है। इसलिए <math>AB</math> कोण <math>\angle A</math> से सटी हुई भुजा है। | ||
समकोण त्रिभुज <math>\triangle ABC</math> में कोण <math>\angle A</math> के त्रिकोणमितीय अनुपात निम्नानुसार परिभाषित किए गए हैं। | समकोण त्रिभुज <math>\triangle ABC</math> में कोण <math>\angle A</math> के त्रिकोणमितीय अनुपात निम्नानुसार परिभाषित किए गए हैं। | ||
| Line 28: | Line 28: | ||
यदि कोण समान रहता है तो किसी कोण के त्रिकोणमितीय अनुपातों का मान त्रिभुज की भुजाओं की लंबाई के साथ भिन्न नहीं होता है। | यदि कोण समान रहता है तो किसी कोण के त्रिकोणमितीय अनुपातों का मान त्रिभुज की भुजाओं की लंबाई के साथ भिन्न नहीं होता है। | ||
== त्रिकोणमितीय अनुपात सारणी == | == त्रिकोणमितीय अनुपात सारणी == | ||
त्रिकोणमितीय अनुपात सारणी में, हम मानक कोणों <math>0^\circ ,30^\circ,45^\circ,60^\circ ,90^\circ</math> के लिए त्रिकोणमितीय अनुपातों के मानों का उपयोग करते हैं। सारणी के मानों की भविष्यवाणी करना और त्रिकोणमितीय अनुपातों के भीतर और यहां तक कि कोणों के बीच विद्यमान प्रतिरूप(पैटर्न) के लिए त्रिकोणमितीय अनुपात सूत्रों का उपयोग करके विभिन्न अन्य कोणों के लिए त्रिकोणमितीय अनुपातों के मानों की गणना करने के लिए संदर्भ के रूप में सारणी का उपयोग करना आसान है। अब, हम नीचे दी गई सारणी में विशिष्ट कोणों के लिए त्रिकोणमितीय अनुपातों के मान को संक्षेप में प्रस्तुत करेंगे: | त्रिकोणमितीय अनुपात सारणी में, हम मानक कोणों <math>0^\circ ,30^\circ,45^\circ,60^\circ ,90^\circ</math> के लिए त्रिकोणमितीय अनुपातों के मानों का उपयोग करते हैं। सारणी के मानों की भविष्यवाणी करना और त्रिकोणमितीय अनुपातों के भीतर और यहां तक कि कोणों के बीच विद्यमान प्रतिरूप(पैटर्न) के लिए त्रिकोणमितीय अनुपात सूत्रों का उपयोग करके विभिन्न अन्य कोणों के लिए त्रिकोणमितीय अनुपातों के मानों की गणना करने के लिए संदर्भ के रूप में सारणी का उपयोग करना आसान है। अब, हम नीचे दी गई सारणी में विशिष्ट [[कोण|कोणों]] के लिए त्रिकोणमितीय अनुपातों के मान को संक्षेप में प्रस्तुत करेंगे: | ||
{| class="wikitable" | {| class="wikitable" | ||
|+ | |+ | ||
Latest revision as of 08:38, 4 November 2024
परिचय
किसी समकोण त्रिभुज में किन्हीं दो भुजाओं के अनुपात को त्रिकोणमितीय अनुपात या त्रिकोणमितीय अनुपात कहते हैं। समकोण त्रिभुज में न्यून कोण का त्रिकोणमितीय अनुपात उसकी भुजाओं के कोण और लंबाई के बीच संबंध को व्यक्त करता है।
परिभाषा
चित्र 1 में दिखाए गए समकोण त्रिभुज पर विचार करें। यहाँ कोण (कोण ) एक न्यूनकोण है। भुजा कोण के सम्मुख है। इसलिए कोण के विपरीत भुजा है। समकोण त्रिभुज का कर्ण है और भुजा कोण का भाग है। इसलिए कोण से सटी हुई भुजा है।
समकोण त्रिभुज में कोण के त्रिकोणमितीय अनुपात निम्नानुसार परिभाषित किए गए हैं।
ध्यान दें: यहां प्रतीक साइन A का उपयोग ''कोण A की साइन'' के संक्षिप्त रूप के रूप में किया गया है। साइन A, ''साइन'' और "A" का गुणनफल नहीं है। ''साइन'' को A से अलग किया गया है। अन्य त्रिकोणमितीय अनुपात के लिए भी इसी तरह की व्याख्याएं की जाती हैं।
यदि कोण समान रहता है तो किसी कोण के त्रिकोणमितीय अनुपातों का मान त्रिभुज की भुजाओं की लंबाई के साथ भिन्न नहीं होता है।
त्रिकोणमितीय अनुपात सारणी
त्रिकोणमितीय अनुपात सारणी में, हम मानक कोणों के लिए त्रिकोणमितीय अनुपातों के मानों का उपयोग करते हैं। सारणी के मानों की भविष्यवाणी करना और त्रिकोणमितीय अनुपातों के भीतर और यहां तक कि कोणों के बीच विद्यमान प्रतिरूप(पैटर्न) के लिए त्रिकोणमितीय अनुपात सूत्रों का उपयोग करके विभिन्न अन्य कोणों के लिए त्रिकोणमितीय अनुपातों के मानों की गणना करने के लिए संदर्भ के रूप में सारणी का उपयोग करना आसान है। अब, हम नीचे दी गई सारणी में विशिष्ट कोणों के लिए त्रिकोणमितीय अनुपातों के मान को संक्षेप में प्रस्तुत करेंगे:
| - | ||||||||
| - | ||||||||
| परिभाषित नहीं | परिभाषित नहीं | |||||||
| परिभाषित नहीं | परिभाषित नहीं | - | परिभाषित नहीं | |||||
| परिभाषित नहीं | - | परिभाषित नहीं | ||||||
| परिभाषित नहीं | परिभाषित नहीं | परिभाषित नहीं |
पूरक कोणों की त्रिकोणमितीय अनुपात सर्वसमिकाएं
पूरक कोण दो कोणों का एक युग्म है, जिसका योग के समान ोता है। कोण का पूरक ( है। पूरक कोणों के त्रिकोणमितीय अनुपात हैं:
- ।