अंतरिक्ष में रेखा का समीकरण: Difference between revisions
(added content) |
(added internal links) |
||
| Line 1: | Line 1: | ||
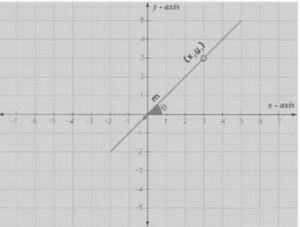
रेखा का समीकरण बिंदुओं के समूह को दर्शाने का एक बीजीय रूप है, जो एक साथ मिलकर एक निर्देशांक प्रणाली में एक रेखा बनाते हैं। निर्देशांक अक्ष में एक साथ मिलकर एक रेखा बनाने वाले असंख्य बिंदुओं को (x, y) के रूप में दर्शाया जाता है और x और y के बीच का संबंध एक बीजीय समीकरण बनाता है, जिसे रेखा का समीकरण कहा जाता है। किसी भी रेखा के समीकरण का उपयोग करके, हम यह पता लगा सकते हैं कि दिया गया बिंदु रेखा पर स्थित है या नहीं। | रेखा का समीकरण बिंदुओं के समूह को दर्शाने का एक बीजीय रूप है, जो एक साथ मिलकर एक निर्देशांक प्रणाली में एक रेखा बनाते हैं। निर्देशांक अक्ष में एक साथ मिलकर एक रेखा बनाने वाले असंख्य बिंदुओं को <math>(x, y)</math> के रूप में दर्शाया जाता है और <math>x</math> और <math>y</math> के बीच का संबंध एक बीजीय समीकरण बनाता है, जिसे रेखा का समीकरण कहा जाता है। किसी भी रेखा के समीकरण का उपयोग करके, हम यह पता लगा सकते हैं कि दिया गया बिंदु रेखा पर स्थित है या नहीं। | ||
रेखा का समीकरण एक | रेखा का समीकरण एक [[प्रथम कोटि एवं प्रथम घात के अवकल समीकरणों को हल करने की विधियाँ|घात]] वाला एक रैखिक समीकरण है। आइए रेखा के समीकरण के विभिन्न रूपों और रेखा के समीकरण को ज्ञात करने के तरीके के बारे में अधिक समझें। | ||
रेखा का समीकरण | == परिभाषा == | ||
रेखा का समीकरण <math>x</math> और <math>y</math> चरों में रैखिक होता है जो रेखा पर प्रत्येक बिंदु <math>(x, y)</math> के निर्देशांकों के बीच संबंध को दर्शाता है। यानी, रेखा का समीकरण उस पर स्थित सभी बिंदुओं से संतुष्ट होता है। | |||
रेखा का समीकरण | [[दो रेखाओं के मध्य न्यूनतम दूरी|रेखा का समीकरण]] रेखा के ढलान और रेखा पर एक बिंदु की सहायता से बनाया जा सकता है। आइए रेखा के ढलान और रेखा पर आवश्यक बिंदु के बारे में अधिक समझें, ताकि रेखा के समीकरण के निर्माण को बेहतर ढंग से समझा जा सके। [[रेखा की ढाल|रेखा का ढलान]] सकारात्मक <math>x</math>-अक्ष के साथ रेखा का झुकाव है और इसे संख्यात्मक पूर्णांक, अंश या सकारात्मक <math>x</math>-अक्ष के साथ कोण के स्पर्शरेखा के रूप में व्यक्त किया जाता है। बिंदु <math>x</math> निर्देशांक और <math>y</math> निर्देशांक के साथ रेखा पर एक बिंदु को संदर्भित करता है | ||
ढलान <math>m</math> वाली और बिंदु <math>(x_1, y_1)</math> से गुजरने वाली रेखा के समीकरण का अभिलम्ब रूप इस प्रकार दिया गया है: <math>y - y_1 = m(x - x_1)</math><math>y - y_1 = m(x - x_1)</math>। इसके अतिरिक्त, इस समीकरण को हल किया जा सकता है और इसे रेखा के समीकरण के मानक रूप / ढलान-अवरोधन रूप / अवरोधन रूप में सरलीकृत किया जा सकता है। | |||
[[File:अंतरिक्ष में रेखा का समीकरण.jpg|thumb|अंतरिक्ष में रेखा का समीकरण]] | |||
== रेखा के समीकरण का मानक रूप == | |||
रेखा के समीकरण का मानक रूप <math>ax + by + c = 0</math> है। यहाँ <math>a, b</math> गुणांक हैं, <math>x</math>, <math>y</math> चर हैं, और <math>c </math> स्थिर पद है। यह एक घात एक समीकरण है, जिसमें चर <math>x</math> और <math>y</math> हैं। <math>x</math> और <math>y</math> के मान निर्देशांक तल में दर्शाई गई रेखा पर बिंदु के निर्देशांक दर्शाते हैं। रेखा के समीकरण के इस मानक रूप को लिखने की प्रक्रिया में निम्नलिखित त्वरित नियमों का पालन किया जाना चाहिए। | |||
सबसे पहले <math>x</math> पद लिखा जाता है, उसके बाद <math>y</math>-पद और अंत में स्थिर पद लिखा जाता है। | |||
गुणांक और स्थिर मानों को भिन्न या दशमलव के रूप में नहीं लिखा जाना चाहिए और उन्हें [[पूर्णांक]] के रूप में लिखा जाना चाहिए। | |||
<math>x</math> के गुणांक '<math>a </math>' का मान सदैव एक धनात्मक पूर्णांक के रूप में लिखा जाता है। | |||
मानक रूप में रेखा का समीकरण: <math>ax + by + c = 0</math> | |||
मानक रूप में रेखा का समीकरण: ax + by + c = 0 | |||
जहाँ, | जहाँ, | ||
a, b गुणांक हैं | <math>a, b</math> गुणांक हैं | ||
<math>x</math>, y चर हैं | |||
<math>c </math> स्थिर है | |||
== रेखा का समीकरण सूत्र == | |||
रेखा के लिए ज्ञात मापदंडों के आधार पर रेखा के समीकरण को लिखने के लगभग पाँच मूल सूत्र हैं। रेखा के समीकरण को खोजने और दर्शाने के लिए उपयोग किए जाने वाले ये विभिन्न सूत्र नीचे दिए गए हैं, | |||
* बिंदु ढलान रूप: <math>(y - y_1) = m(x - x_1)</math> | |||
* दो बिन्दु रूप: <math>(y -y_1) =[(y_2 - y_1) / (x_2 - x_1)] (x - x_1)</math> | |||
* ढलान अवरोधन रूप: <math>y = mx + c</math> | |||
* अवरोधन रूप: <math>x/a + y/b = 1</math> | |||
* अभिलम्ब रूप: <math>x \ cos \theta + y\ sin \theta = p</math> | |||
रेखा के समीकरण के | आइये हम रेखा के समीकरण के प्रत्येक रूप के बारे में अधिक जानने का प्रयास करें। | ||
( | === रेखा के समीकरण का बिंदु ढलान रूप === | ||
रेखा के समीकरण के बिंदु-ढलान रूप के लिए रेखा पर एक बिंदु और रेखा का ढलान आवश्यक है। यदि <math>(x_1, y_1)</math> रेखा पर एक बिंदु है और रेखा का ढलान <math>m</math> है, तो बिंदु-ढलान रूप में रेखा का समीकरण है: | |||
<math>(y - y_1) = m(x - x_1)</math> | |||
रेखा | यहाँ <math>m =</math> रेखा का ढलान है और रेखा का ढलान धनात्मक, ऋणात्मक या शून्य ढलान हो सकता है। | ||
रेखा के समीकरण का दो बिंदु रूप रेखा के समीकरण के बिंदु-ढलान रूप का विस्तार है। रेखा के समीकरण के बिंदु-ढलान रूप में ढलान m = ( | === रेखा के समीकरण का दो बिंदु रूप === | ||
रेखा के समीकरण का दो बिंदु रूप रेखा के समीकरण के बिंदु-ढलान रूप का विस्तार है। रेखा के समीकरण के बिंदु-ढलान रूप में ढलान<math>m = (y_2 - y_1)/(x_2 - x_1)</math> को रेखा के समीकरण के दो बिंदु रूप में प्रतिस्थापित किया जाता है। दो बिंदुओं <math>(x_1, y_1)</math> और <math>(x_2 , y_2 )</math> से रेखा समीकरण दो-बिंदु रूप द्वारा दिया गया है, जो इस प्रकार है। | |||
(y - | <math>(y -y_1) =[(y_2 - y_1) / (x_2 - x_1)] (x - x_1)</math> | ||
रेखा के समीकरण का ढलान अवरोधन रूप | === रेखा के समीकरण का ढलान अवरोधन रूप === | ||
रेखा का ढलान-अवरोधन रूप <math>y = mx + c</math> है। यहाँ <math>m</math> रेखा का ढलान है और '<math>c </math>' रेखा का <math>y</math>-अवरोधन है। यह रेखा <math>y</math>-अक्ष को बिंदु <math>(0, c)</math> पर प्रतिच्छेद करती है और <math>c </math> मूल बिंदु से <math>y</math>-अक्ष पर इस बिंदु की दूरी है। रेखा के समीकरण का ढलान-अवरोधन रूप महत्वपूर्ण है और गणित और इंजीनियरिंग के विभिन्न विषयों में इसके बहुत अच्छे अनुप्रयोग हैं। | |||
<math>y = mx + c</math> | |||
y | === रेखा के समीकरण का अवरोधन रूप === | ||
अंतर्खंड रूप में रेखा का समीकरण <math>x</math>-अवरोधन '<math>a </math>' और <math>y</math>-अवरोधन '<math>b </math>' के साथ बनता है। रेखा <math>x</math>-अक्ष को बिंदु <math>(a, 0)</math> पर तथा <math>y</math>-अक्ष को बिंदु<math>(0, b)</math> पर प्रतिच्छेद करती है, तथा <math>a, b</math> मूल बिंदु से इन बिंदुओं की क्रमशः दूरियाँ हैं। इसके अलावा, इन दो बिंदुओं को रेखा के समीकरण के दो-बिंदु रूप में प्रतिस्थापित किया जा सकता है तथा रेखा के समीकरण के इस अवरोधन रूप को प्राप्त करने के लिए सरलीकृत किया जा सकता है। अवरोधन रूप में रेखा का समीकरण है: | |||
<math>x/a + y/b = 1</math> | |||
=== अभिलम्ब रूप का उपयोग करके रेखा का समीकरण === | |||
रेखा के समीकरण का अभिलम्ब रूप मूल बिंदु से रेखा पर खींचे गए लंब पर आधारित होता है। दी गई रेखा के लंबवत और मूल बिंदु से गुजरने वाली रेखा को अभिलम्ब कहा जाता है। यहाँ अभिलम्ब '<math>p </math>' की लंबाई और अभिलम्ब 'θ' द्वारा धनात्मक <math>x</math>-अक्ष के साथ बनाया गया कोण रेखा के समीकरण को बनाने के लिए उपयोगी है। रेखा के समीकरण का अभिलम्ब रूप इस प्रकार है: | |||
x | <math>x\ cos \theta + y \ sin \theta = p</math> | ||
यह भी देखें: इसके अलावा, रेखा के समीकरण के ऊपर परिभाषित रूपों के अलावा, हम रेखा के समीकरण कैलकुलेटर का उपयोग करके त्वरित और आसान चरणों में रेखा के समीकरण को आसानी से पा सकते हैं। साथ ही, रेखा के समीकरण कैलकुलेटर का उपयोग करने के लिए, हमें ढलान <math>m</math> और <math>y</math>-अवरोध <math>c </math> के मान प्रदान करने की आवश्यकता है, ताकि ढलान-अवरोधन रूप और मानक रूप में रेखा के समीकरण का उत्तर प्राप्त किया जा सके। | |||
रेखा | == रेखा का समीकरण ज्ञात करने की विधि == | ||
किसी रेखा का समीकरण ज्ञात करने के लिए, हम अपने ज्ञात आंकड़ों के आधार पर ऊपर बताए गए किसी भी रूप के लिए सूत्र लागू कर सकते हैं। ज्ञात मापदंडों और रूप के आधार पर विभिन्न मामलों के लिए अनुसरण किए जा सकने वाले चरण नीचे दिए गए हैं, | |||
चरण 1: दिए गए आंकड़ों को नोट करें, रेखा का ढलान '<math>m </math>' के रूप में और दिए गए बिंदु(ओं) के निर्देशांक <math>(x_n, y_n)</math> के रूप में। | |||
चरण 1: दिए गए | |||
चरण 2: दिए गए मापदंडों के आधार पर आवश्यक सूत्र लागू करें, | चरण 2: दिए गए मापदंडों के आधार पर आवश्यक सूत्र लागू करें, | ||
(i) किसी रेखा का समीकरण ज्ञात करने के लिए, उसका ढलान या ढाल और y-अक्ष पर उसका अवरोधन दिया गया है, ढलान-अवरोधन रूप का उपयोग करें। | (i) किसी रेखा का समीकरण ज्ञात करने के लिए, उसका ढलान या ढाल और <math>y</math>-अक्ष पर उसका अवरोधन दिया गया है, ढलान-अवरोधन रूप का उपयोग करें। | ||
(ii) किसी रेखा का समीकरण ज्ञात करने के लिए, उसका ढलान और रेखा पर स्थित एक बिंदु के निर्देशांक दिए गए हैं, बिंदु-ढलान रूप का उपयोग करें। | (ii) किसी रेखा का समीकरण ज्ञात करने के लिए, उसका ढलान और रेखा पर स्थित एक बिंदु के निर्देशांक दिए गए हैं, बिंदु-ढलान रूप का उपयोग करें। | ||
| Line 90: | Line 83: | ||
(iii) किसी रेखा का समीकरण ज्ञात करने के लिए, उस पर स्थित दो बिंदुओं के निर्देशांक दिए गए हैं, दो-बिंदु रूप का उपयोग करें। | (iii) किसी रेखा का समीकरण ज्ञात करने के लिए, उस पर स्थित दो बिंदुओं के निर्देशांक दिए गए हैं, दो-बिंदु रूप का उपयोग करें। | ||
(iv) समीकरण लिखने के लिए, x-अवरोधन और y-अवरोधन दिया गया है, अवरोधन रूप का उपयोग करें। | (iv) समीकरण लिखने के लिए, <math>x</math>-अवरोधन और <math>y</math>-अवरोधन दिया गया है, अवरोधन रूप का उपयोग करें। | ||
चरण 3: रेखा के समीकरण को मानक रूप में व्यक्त करने के लिए पदों को पुनर्व्यवस्थित करें। | चरण 3: रेखा के समीकरण को मानक रूप में व्यक्त करने के लिए पदों को पुनर्व्यवस्थित करें। | ||
नोट: मामले (ii), (iii) और (iv) के लिए वैकल्पिक विधि पहले दिए गए | नोट: मामले (ii), (iii) और (iv) के लिए वैकल्पिक विधि पहले दिए गए आंकड़ों का उपयोग करके ढलान सूत्र को लागू करके ढलान की गणना करना और फिर अंत में ढलान-अवरोधन सूत्र को लागू करना हो सकता है। | ||
== महत्वपूर्ण टिप्पणियाँ == | |||
ax + by + c = 0 के समांतर एक रेखा का समीकरण ax + by + k = 0 है। | * <math>x</math>-अक्ष का समीकरण <math>y = 0</math> है और <math>y</math>-अक्ष का समीकरण <math>x = 0</math> है। | ||
* <math>x</math>-अक्ष के समांतर एक रेखा का समीकरण <math>y = b</math> है, जहाँ यह <math>y</math>-अक्ष को बिंदु <math>(0, b)</math> पर प्रतिच्छेद करती है। | |||
* <math>y</math>-अक्ष के समांतर एक रेखा का समीकरण <math>x = a</math> है, जहाँ यह <math>x</math>-अक्ष को बिंदु <math>(a, 0)</math>पर प्रतिच्छेद करती है। | |||
* <math>ax + by + c = 0</math> के समांतर एक रेखा का समीकरण <math>ax + by + k = 0</math> है। | |||
* <math>ax + by + c = 0</math> के लंबवत एक रेखा का समीकरण <math>bx - ay + k = 0</math> है। | |||
[[Category:त्रि-विमीय ज्यामिति]][[Category:गणित]][[Category:कक्षा-12]] | [[Category:त्रि-विमीय ज्यामिति]][[Category:गणित]][[Category:कक्षा-12]] | ||
Latest revision as of 10:23, 18 December 2024
रेखा का समीकरण बिंदुओं के समूह को दर्शाने का एक बीजीय रूप है, जो एक साथ मिलकर एक निर्देशांक प्रणाली में एक रेखा बनाते हैं। निर्देशांक अक्ष में एक साथ मिलकर एक रेखा बनाने वाले असंख्य बिंदुओं को के रूप में दर्शाया जाता है और और के बीच का संबंध एक बीजीय समीकरण बनाता है, जिसे रेखा का समीकरण कहा जाता है। किसी भी रेखा के समीकरण का उपयोग करके, हम यह पता लगा सकते हैं कि दिया गया बिंदु रेखा पर स्थित है या नहीं।
रेखा का समीकरण एक घात वाला एक रैखिक समीकरण है। आइए रेखा के समीकरण के विभिन्न रूपों और रेखा के समीकरण को ज्ञात करने के तरीके के बारे में अधिक समझें।
परिभाषा
रेखा का समीकरण और चरों में रैखिक होता है जो रेखा पर प्रत्येक बिंदु के निर्देशांकों के बीच संबंध को दर्शाता है। यानी, रेखा का समीकरण उस पर स्थित सभी बिंदुओं से संतुष्ट होता है।
रेखा का समीकरण रेखा के ढलान और रेखा पर एक बिंदु की सहायता से बनाया जा सकता है। आइए रेखा के ढलान और रेखा पर आवश्यक बिंदु के बारे में अधिक समझें, ताकि रेखा के समीकरण के निर्माण को बेहतर ढंग से समझा जा सके। रेखा का ढलान सकारात्मक -अक्ष के साथ रेखा का झुकाव है और इसे संख्यात्मक पूर्णांक, अंश या सकारात्मक -अक्ष के साथ कोण के स्पर्शरेखा के रूप में व्यक्त किया जाता है। बिंदु निर्देशांक और निर्देशांक के साथ रेखा पर एक बिंदु को संदर्भित करता है
ढलान वाली और बिंदु से गुजरने वाली रेखा के समीकरण का अभिलम्ब रूप इस प्रकार दिया गया है: । इसके अतिरिक्त, इस समीकरण को हल किया जा सकता है और इसे रेखा के समीकरण के मानक रूप / ढलान-अवरोधन रूप / अवरोधन रूप में सरलीकृत किया जा सकता है।
रेखा के समीकरण का मानक रूप
रेखा के समीकरण का मानक रूप है। यहाँ गुणांक हैं, , चर हैं, और स्थिर पद है। यह एक घात एक समीकरण है, जिसमें चर और हैं। और के मान निर्देशांक तल में दर्शाई गई रेखा पर बिंदु के निर्देशांक दर्शाते हैं। रेखा के समीकरण के इस मानक रूप को लिखने की प्रक्रिया में निम्नलिखित त्वरित नियमों का पालन किया जाना चाहिए।
सबसे पहले पद लिखा जाता है, उसके बाद -पद और अंत में स्थिर पद लिखा जाता है।
गुणांक और स्थिर मानों को भिन्न या दशमलव के रूप में नहीं लिखा जाना चाहिए और उन्हें पूर्णांक के रूप में लिखा जाना चाहिए।
के गुणांक '' का मान सदैव एक धनात्मक पूर्णांक के रूप में लिखा जाता है।
मानक रूप में रेखा का समीकरण:
जहाँ,
गुणांक हैं
, y चर हैं
स्थिर है
रेखा का समीकरण सूत्र
रेखा के लिए ज्ञात मापदंडों के आधार पर रेखा के समीकरण को लिखने के लगभग पाँच मूल सूत्र हैं। रेखा के समीकरण को खोजने और दर्शाने के लिए उपयोग किए जाने वाले ये विभिन्न सूत्र नीचे दिए गए हैं,
- बिंदु ढलान रूप:
- दो बिन्दु रूप:
- ढलान अवरोधन रूप:
- अवरोधन रूप:
- अभिलम्ब रूप:
आइये हम रेखा के समीकरण के प्रत्येक रूप के बारे में अधिक जानने का प्रयास करें।
रेखा के समीकरण का बिंदु ढलान रूप
रेखा के समीकरण के बिंदु-ढलान रूप के लिए रेखा पर एक बिंदु और रेखा का ढलान आवश्यक है। यदि रेखा पर एक बिंदु है और रेखा का ढलान है, तो बिंदु-ढलान रूप में रेखा का समीकरण है:
यहाँ रेखा का ढलान है और रेखा का ढलान धनात्मक, ऋणात्मक या शून्य ढलान हो सकता है।
रेखा के समीकरण का दो बिंदु रूप
रेखा के समीकरण का दो बिंदु रूप रेखा के समीकरण के बिंदु-ढलान रूप का विस्तार है। रेखा के समीकरण के बिंदु-ढलान रूप में ढलान को रेखा के समीकरण के दो बिंदु रूप में प्रतिस्थापित किया जाता है। दो बिंदुओं और से रेखा समीकरण दो-बिंदु रूप द्वारा दिया गया है, जो इस प्रकार है।
रेखा के समीकरण का ढलान अवरोधन रूप
रेखा का ढलान-अवरोधन रूप है। यहाँ रेखा का ढलान है और '' रेखा का -अवरोधन है। यह रेखा -अक्ष को बिंदु पर प्रतिच्छेद करती है और मूल बिंदु से -अक्ष पर इस बिंदु की दूरी है। रेखा के समीकरण का ढलान-अवरोधन रूप महत्वपूर्ण है और गणित और इंजीनियरिंग के विभिन्न विषयों में इसके बहुत अच्छे अनुप्रयोग हैं।
रेखा के समीकरण का अवरोधन रूप
अंतर्खंड रूप में रेखा का समीकरण -अवरोधन '' और -अवरोधन '' के साथ बनता है। रेखा -अक्ष को बिंदु पर तथा -अक्ष को बिंदु पर प्रतिच्छेद करती है, तथा मूल बिंदु से इन बिंदुओं की क्रमशः दूरियाँ हैं। इसके अलावा, इन दो बिंदुओं को रेखा के समीकरण के दो-बिंदु रूप में प्रतिस्थापित किया जा सकता है तथा रेखा के समीकरण के इस अवरोधन रूप को प्राप्त करने के लिए सरलीकृत किया जा सकता है। अवरोधन रूप में रेखा का समीकरण है:
अभिलम्ब रूप का उपयोग करके रेखा का समीकरण
रेखा के समीकरण का अभिलम्ब रूप मूल बिंदु से रेखा पर खींचे गए लंब पर आधारित होता है। दी गई रेखा के लंबवत और मूल बिंदु से गुजरने वाली रेखा को अभिलम्ब कहा जाता है। यहाँ अभिलम्ब '' की लंबाई और अभिलम्ब 'θ' द्वारा धनात्मक -अक्ष के साथ बनाया गया कोण रेखा के समीकरण को बनाने के लिए उपयोगी है। रेखा के समीकरण का अभिलम्ब रूप इस प्रकार है:
यह भी देखें: इसके अलावा, रेखा के समीकरण के ऊपर परिभाषित रूपों के अलावा, हम रेखा के समीकरण कैलकुलेटर का उपयोग करके त्वरित और आसान चरणों में रेखा के समीकरण को आसानी से पा सकते हैं। साथ ही, रेखा के समीकरण कैलकुलेटर का उपयोग करने के लिए, हमें ढलान और -अवरोध के मान प्रदान करने की आवश्यकता है, ताकि ढलान-अवरोधन रूप और मानक रूप में रेखा के समीकरण का उत्तर प्राप्त किया जा सके।
रेखा का समीकरण ज्ञात करने की विधि
किसी रेखा का समीकरण ज्ञात करने के लिए, हम अपने ज्ञात आंकड़ों के आधार पर ऊपर बताए गए किसी भी रूप के लिए सूत्र लागू कर सकते हैं। ज्ञात मापदंडों और रूप के आधार पर विभिन्न मामलों के लिए अनुसरण किए जा सकने वाले चरण नीचे दिए गए हैं,
चरण 1: दिए गए आंकड़ों को नोट करें, रेखा का ढलान '' के रूप में और दिए गए बिंदु(ओं) के निर्देशांक के रूप में।
चरण 2: दिए गए मापदंडों के आधार पर आवश्यक सूत्र लागू करें,
(i) किसी रेखा का समीकरण ज्ञात करने के लिए, उसका ढलान या ढाल और -अक्ष पर उसका अवरोधन दिया गया है, ढलान-अवरोधन रूप का उपयोग करें।
(ii) किसी रेखा का समीकरण ज्ञात करने के लिए, उसका ढलान और रेखा पर स्थित एक बिंदु के निर्देशांक दिए गए हैं, बिंदु-ढलान रूप का उपयोग करें।
(iii) किसी रेखा का समीकरण ज्ञात करने के लिए, उस पर स्थित दो बिंदुओं के निर्देशांक दिए गए हैं, दो-बिंदु रूप का उपयोग करें।
(iv) समीकरण लिखने के लिए, -अवरोधन और -अवरोधन दिया गया है, अवरोधन रूप का उपयोग करें।
चरण 3: रेखा के समीकरण को मानक रूप में व्यक्त करने के लिए पदों को पुनर्व्यवस्थित करें।
नोट: मामले (ii), (iii) और (iv) के लिए वैकल्पिक विधि पहले दिए गए आंकड़ों का उपयोग करके ढलान सूत्र को लागू करके ढलान की गणना करना और फिर अंत में ढलान-अवरोधन सूत्र को लागू करना हो सकता है।
महत्वपूर्ण टिप्पणियाँ
- -अक्ष का समीकरण है और -अक्ष का समीकरण है।
- -अक्ष के समांतर एक रेखा का समीकरण है, जहाँ यह -अक्ष को बिंदु पर प्रतिच्छेद करती है।
- -अक्ष के समांतर एक रेखा का समीकरण है, जहाँ यह -अक्ष को बिंदु पर प्रतिच्छेद करती है।
- के समांतर एक रेखा का समीकरण है।
- के लंबवत एक रेखा का समीकरण है।