कोण- परिभाषाएँ: Difference between revisions

Revision as of 16:04, 6 June 2024

ज्यामिति में, रेखाएँ और कोण मूल शब्द हैं जो विषय की नींव स्थापित करते हैं। कोण को दो किरणों द्वारा बनाई गई एक आकृति के रूप में परिभाषित किया जाता है जो एक सामान्य समापन बिंदु पर मिलती हैं। इन्हें एक चांदे(प्रोट्रैक्टर) का उपयोग करके डिग्री में मापा जाता है। सभी ज्यामितीय आकृतियों में रेखाएँ और कोण होते हैं।

कोण

An angle is formed when two rays originate from the same end point. The rays making an angle are called the arms of the angle and the end point is called the vertex of the angle.

Angles are usually measured in degrees and denoted by $^{\circ }$ (the degree symbol), which is a measure of rotation. An angle can have a value between $0^{\circ }$ to $360^{\circ }$ and it is denoted by the symbol $\angle$ . Observe in the Fig. 1 which shows $\angle ABC$

चित्र-1 कोण

कोण के प्रकार

An acute angle measures between $0^{\circ }$ and $90^{\circ }$ , whereas a right angle is exactly equal to $90^{\circ }$ . An angle greater than $90^{\circ }$ but less than $180^{\circ }$ is called an obtuse angle. Straight angle is equal to $180^{\circ }$ . An angle which is greater than $180^{\circ }$ but less than $360^{\circ }$ is called a reflex angle. Two angles whose sum is $90^{\circ }$ are called complementary angles, and two angles whose sum is $180^{\circ }$ are called supplementary angles.

चित्र-2 कोण के प्रकार

आसन्न कोण

Two angles are adjacent, if they have a common vertex, a common arm and their non-common arms are on different sides of the common arm. In Fig. 3, $\angle ABD$ and $\angle DBC$ are adjacent angles. Ray $BD$ is their common arm and point $B$ is their common vertex. Ray $BA$ and ray $BC$ are non common arms. When two angles are adjacent, then their sum is always equal to the angle formed by the two non common arms. So, we can write $\angle ABC=\angle ABD+\angle DBC$ . Note that $\angle ABC$ and $\angle ABD$ are not adjacent angles because their non common arms $BD$ and $BC$ lie on the same side of the common arm $BA$ .

चित्र-3 आसन्न कोण

कोणों का रैखिक युग्म

If the non-common arms $BA$ and $BC$ in Fig. 3 form a line then it will look like Fig. 4. In this case, $\angle ABD$ and $\angle DBC$ are called linear pair of angles.

चित्र-4 कोणों का रैखिक युग्म

शीर्षाभिमुख कोण

Vertically opposite angles formed when two lines, say $AB$ and $CD$ , intersect each other, say at the point $O$ (see Fig. 5). There are two pairs of vertically opposite angles.

$\angle AOD$ and $\angle BOC$

$\angle AOC$ and $\angle DOB$

चित्र-5 शीर्षाभिमुख कोण

@@ Line 1: / Line 1: @@
 ज्यामिति में, रेखाएँ और कोण मूल शब्द हैं जो विषय की नींव स्थापित करते हैं। कोण को दो किरणों द्वारा बनाई गई एक आकृति के रूप में परिभाषित किया जाता है जो एक सामान्य समापन बिंदु पर मिलती हैं। इन्हें एक चांदे(प्रोट्रैक्टर) का उपयोग करके डिग्री में मापा जाता है। सभी ज्यामितीय आकृतियों में रेखाएँ और कोण होते हैं।
-== Angles ==
+== कोण ==
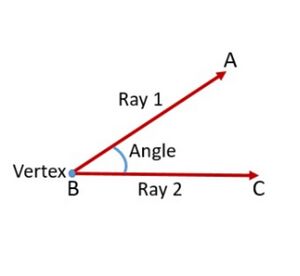
 An angle is formed when two rays originate from the same end point. The rays making an angle are called the arms of the angle and the end point is called the vertex of the angle.
 Angles are usually measured in degrees and denoted by <math>^\circ</math> (the degree symbol), which is a measure of rotation. An angle can have a value between <math>0^\circ</math> to <math>360^\circ</math> and it is denoted by the symbol <math>\angle</math>. Observe in the Fig. 1 which shows <math>\angle ABC</math>
-[[File:Angle.jpg|alt=Fig.1 Angle|none|thumb|Fig.1 Angle]]
+[[File:Angle.jpg|alt=Fig.1 Angle|none|thumb|चित्र-1 कोण]]
-== Types of Angles ==
+== कोण के प्रकार ==
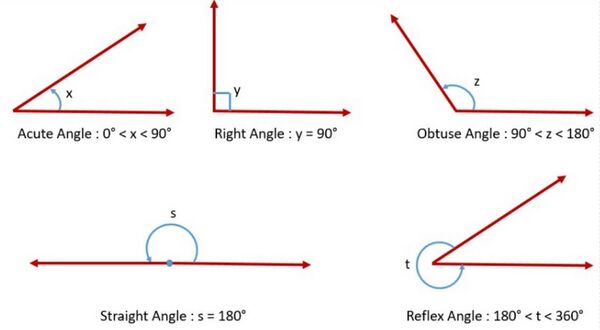
-An acute angle measures between <math>0^\circ</math> and <math>90^\circ</math>, whereas a right angle is exactly equal to <math>90^\circ</math>. An angle greater than <math>90^\circ</math> but less than <math>180^\circ</math> is called an obtuse angle. Straight angle is equal to <math>180^\circ</math>. An angle which is greater than <math>180^\circ</math> but less than <math>360^\circ</math> is called a reflex angle. Two angles whose sum is <math>90^\circ</math> are called complementary angles, and two angles whose sum is <math>180^\circ</math> are called supplementary angles. [[File:Types of Angles.jpg|alt=Fig.2 Types of Angles|none|thumb|600x600px|Fig.2 Types of Angles]]
+An acute angle measures between <math>0^\circ</math> and <math>90^\circ</math>, whereas a right angle is exactly equal to <math>90^\circ</math>. An angle greater than <math>90^\circ</math> but less than <math>180^\circ</math> is called an obtuse angle. Straight angle is equal to <math>180^\circ</math>. An angle which is greater than <math>180^\circ</math> but less than <math>360^\circ</math> is called a reflex angle. Two angles whose sum is <math>90^\circ</math> are called complementary angles, and two angles whose sum is <math>180^\circ</math> are called supplementary angles. [[File:Types of Angles.jpg|alt=Fig.2 Types of Angles|none|thumb|600x600px|चित्र-2 कोण के प्रकार]]
-== Adjacent angles ==
+== आसन्न कोण ==
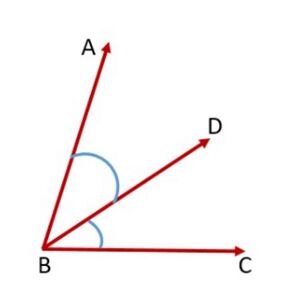
-Two angles are adjacent, if they have a common vertex, a common arm and their non-common arms are on different sides of the common arm. In Fig. 3, <math>\angle ABD</math> and <math>\angle DBC</math> are adjacent angles. Ray <math>BD</math> is their common arm and point <math>B</math> is their common vertex. Ray <math>BA</math> and ray <math>BC</math> are non common arms. When two angles are adjacent, then their sum is always equal to the angle formed by the two non common arms. So, we can write <math>\angle ABC =\angle ABD +\angle DBC</math>. Note that <math>\angle ABC</math> and <math>\angle ABD</math> are not adjacent angles because their non common arms <math>BD</math> and <math>BC</math> lie on the same side of the common arm <math>BA</math>.[[File:Adjacent angles.jpg|alt=Fig. 3 Adjacent angles|none|thumb|Fig. 3 Adjacent angles]]
+Two angles are adjacent, if they have a common vertex, a common arm and their non-common arms are on different sides of the common arm. In Fig. 3, <math>\angle ABD</math> and <math>\angle DBC</math> are adjacent angles. Ray <math>BD</math> is their common arm and point <math>B</math> is their common vertex. Ray <math>BA</math> and ray <math>BC</math> are non common arms. When two angles are adjacent, then their sum is always equal to the angle formed by the two non common arms. So, we can write <math>\angle ABC =\angle ABD +\angle DBC</math>. Note that <math>\angle ABC</math> and <math>\angle ABD</math> are not adjacent angles because their non common arms <math>BD</math> and <math>BC</math> lie on the same side of the common arm <math>BA</math>.[[File:Adjacent angles.jpg|alt=Fig. 3 Adjacent angles|none|thumb|चित्र-3 आसन्न कोण]]
-== Linear pair of angles ==
+== कोणों का रैखिक युग्म ==
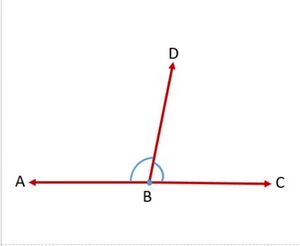
-If the non-common arms <math>BA</math> and <math>BC</math> in Fig. 3 form a line then it will look like Fig. 4. In this case, <math>\angle ABD</math> and <math>\angle DBC</math> are called linear pair of angles. [[File:Linear Pair of angles.jpg|alt=Fig.4 Linear pair of angles|none|thumb|Fig.4 Linear pair of angles]]
+If the non-common arms <math>BA</math> and <math>BC</math> in Fig. 3 form a line then it will look like Fig. 4. In this case, <math>\angle ABD</math> and <math>\angle DBC</math> are called linear pair of angles. [[File:Linear Pair of angles.jpg|alt=Fig.4 Linear pair of angles|none|thumb|चित्र-4 कोणों का रैखिक युग्म]]
-== Vertically opposite angles ==
+== शीर्षाभिमुख कोण ==
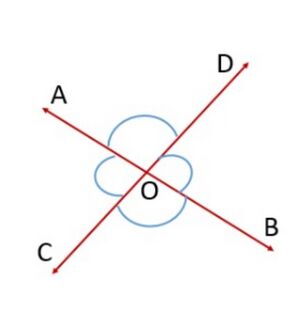
 Vertically opposite angles formed when two lines, say <math>AB</math> and <math>CD</math>, intersect each other, say at the point <math>O</math> (see Fig. 5). There are two pairs of vertically opposite angles.
 <math>\angle AOD</math> and <math>\angle BOC</math>
-<math>\angle AOC</math> and <math>\angle DOB</math>[[File:Vertically opposite angles.jpg|alt=Fig. 5 Vertically opposite angles|none|thumb|Fig. 5 Vertically opposite angles]]
+<math>\angle AOC</math> and <math>\angle DOB</math>[[File:Vertically opposite angles.jpg|alt=Fig. 5 Vertically opposite angles|none|thumb|चित्र-5 शीर्षाभिमुख कोण]]
 [[Category:रेखाएँ और कोण]]
 [[Category:कक्षा-9]]
 [[Category:गणित]]