कोण- परिभाषाएँ
ज्यामिति में, रेखाएँ और कोण मूल शब्द हैं जो विषय की नींव स्थापित करते हैं। कोण को दो किरणों द्वारा बनाई गई एक आकृति के रूप में परिभाषित किया जाता है जो एक सामान्य समापन बिंदु पर मिलती हैं। इन्हें एक चांदे(प्रोट्रैक्टर) का उपयोग करके डिग्री में मापा जाता है। सभी ज्यामितीय आकृतियों में रेखाएँ और कोण होते हैं।
कोण
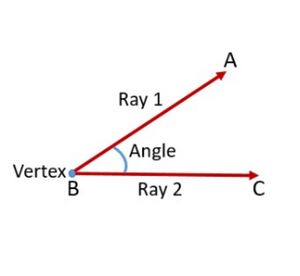
जब दो किरणें एक ही अंतिम बिंदु से निकलती हैं तो कोण बनता है। कोण बनाने वाली किरणें कोण की भुजाएं कहलाती हैं और अंतिम बिंदु कोण का शीर्ष कहलाता है।
कोणों को साधारणतः डिग्री में मापा जाता है और (डिग्री प्रतीक) द्वारा दर्शाया जाता है, जो घूर्णन का एक माप है। कोण का मान से के बीच हो सकता है और इसे प्रतीक द्वारा दर्शाया जाता है। चित्र 1 में देखें जो दर्शाता है।
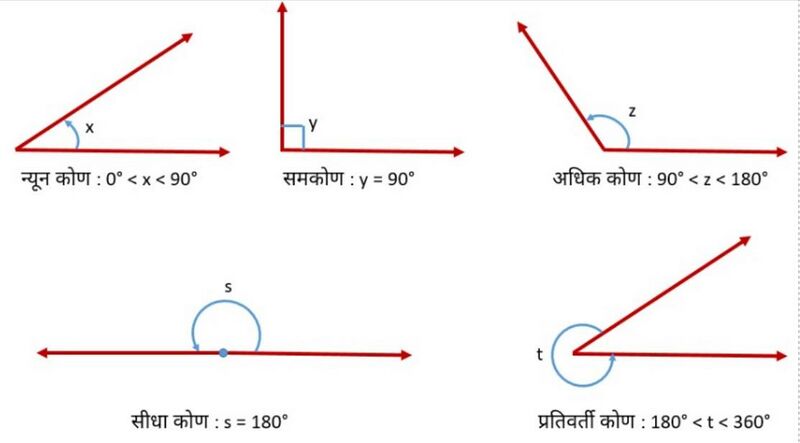
कोण के प्रकार
न्यून कोण का माप और के बीच होता है, जबकि समकोण के बराबर होता है। से बड़ा लेकिन से छोटा कोण अधिक कोण कहलाता है। सीधा कोण के बराबर होता है। वह कोण जो से अधिक लेकिन से कम हो, प्रतिवर्ती कोण कहलाता है। दो कोण जिनका योग है, पूरक कोण कहलाते हैं तथा दो कोण जिनका योग है, संपूरक कोण कहलाते हैं।
आसन्न कोण
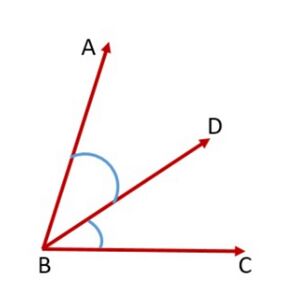
दो कोण आसन्न होते हैं, यदि उनका एक उभयनिष्ठ शीर्ष, एक उभयनिष्ठ भुजा हो और उनकी गैर-उभयनिष्ठ भुजाएँ उभयनिष्ठ भुजा के विभिन्न पक्षों पर हों। चित्र-3 में, और आसन्न कोण हैं। किरण उनकी उभयनिष्ठ भुजा है और बिंदु उनका उभयनिष्ठ शीर्ष है। किरण और किरण गैर-उभयनिष्ठ भुजाएँ हैं। जब दो कोण आसन्न होते हैं, तो उनका योग हमेशा दो गैर-उभयनिष्ठ भुजाओं द्वारा बनाए गए कोण के बराबर होता है। इसलिए, हम लिख सकते हैं। ध्यान दें कि और आसन्न कोण नहीं हैं क्योंकि उनकी गैर-उभयनिष्ठ भुजाएँ और सामान्य भुजा के एक ही ओर स्थित हैं।
कोणों का रैखिक युग्म
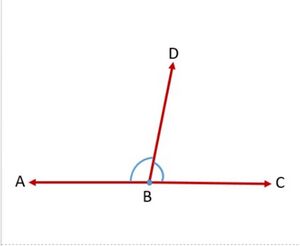
यदि चित्र-3 में गैर-उभयनिष्ठ भुजाएँ और एक रेखा बनाते हैं तो यह चित्र-4 जैसा दिखाई देगा। इस स्थिति में, और कोणों के रैखिक युग्म कहलाते हैं .
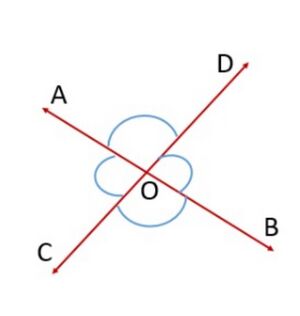
शीर्षाभिमुख कोण
शीर्षाभिमुख कोण तब बनते हैं जब दो रेखाएँ, मान लीजिए और , एक दूसरे को बिंदु पर प्रतिच्छेद करती हैं (चित्र-5 देखें)। शीर्षाभिमुख कोणों के दो युग्म हैं।
and
and