समान जीवाएं और उनकी केंद्र से दूरीयाँ: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
A chord is the line segment which joins two points on the circumference of a circle. In general, a circle can have infinitely many chords. The distance of the line from a point is defined as the perpendicular distance from a point to a line. If we draw infinite chords to a circle, the longer chord is close to the centre of the circle, than the smaller chord of a circle. Here we will discuss the theorem and proof related to the equal chords and their distance from the centre and also its converse theorem in detail. | |||
== Equal Chords and their Distance from the Centre – Theorem and Proof == | |||
=== Theorem: === | |||
Equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres). | |||
'''Proof:''' | |||
[[File:Circle-2.jpg|alt=Fig. 2|thumb|150x150px|Fig. 2]] | |||
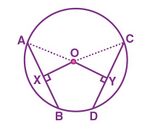
Consider a circle with centre <math>O</math>. | |||
<math>AB</math> and <math>CD</math> are the equal chords of a circle i.e <math>AB=CD</math> | |||
The line <math>OX</math> is perpendicular to the chord <math>AB</math> and <math>OY</math> is perpendicular to the chord <math>CD</math>. | |||
We have to prove <math>OX=OY</math>. | |||
Also, the line <math>OX</math> is perpendicular to <math>AB</math>. | |||
As the perpendicular from the centre of the circle to a chord, bisects the chord, we can write it as | |||
<math>AX=BX=\frac{AB}{2} .... (1)</math> | |||
Similarly, the line <math>OY</math> is perpendicular to <math>CD</math>, | |||
<math>CY=DY=\frac{CD}{2} .... (2)</math> [Since, the perpendicular from the centre of the circle to a chord, bisects the chord) | |||
Given that, <math>AB=CD</math> | |||
<math>\frac{AB}{2}=\frac{CD}{2} .... (2)</math> | |||
Therefore, <math>AX=CY .... (3)</math> [Using <math>(1)</math> and <math>(2)</math>] | |||
Now, by using the triangles <math>AOX</math> and <math>COY</math> , | |||
<math>\angle OXA =\angle OYC =90^\circ </math> | |||
<math>OA =OC </math> (Radii) | |||
<math>AX=CY .... (3)</math> | |||
From the RHS rule, we can write it as | |||
<math>\triangle AOX \cong \triangle COY</math> | |||
Hence, we can conclude that <math>OX=OY</math>(Using CPCT) | |||
Therefore, the theorem “equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres)”, is proved. | |||
=== Converse of this Theorem === | |||
The converse of the above-mentioned theorem is “chords equidistant from the centre of a circle are equal in length”. | |||
[[Category:वृत्त]][[Category:कक्षा-9]][[Category:गणित]] | [[Category:वृत्त]][[Category:कक्षा-9]][[Category:गणित]] | ||
Revision as of 12:06, 18 September 2024
A chord is the line segment which joins two points on the circumference of a circle. In general, a circle can have infinitely many chords. The distance of the line from a point is defined as the perpendicular distance from a point to a line. If we draw infinite chords to a circle, the longer chord is close to the centre of the circle, than the smaller chord of a circle. Here we will discuss the theorem and proof related to the equal chords and their distance from the centre and also its converse theorem in detail.
Equal Chords and their Distance from the Centre – Theorem and Proof
Theorem:
Equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres).
Proof:
Consider a circle with centre .
and are the equal chords of a circle i.e
The line is perpendicular to the chord and is perpendicular to the chord .
We have to prove .
Also, the line is perpendicular to .
As the perpendicular from the centre of the circle to a chord, bisects the chord, we can write it as
Similarly, the line is perpendicular to ,
[Since, the perpendicular from the centre of the circle to a chord, bisects the chord)
Given that,
Therefore, [Using and ]
Now, by using the triangles and ,
(Radii)
From the RHS rule, we can write it as
Hence, we can conclude that (Using CPCT)
Therefore, the theorem “equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres)”, is proved.
Converse of this Theorem
The converse of the above-mentioned theorem is “chords equidistant from the centre of a circle are equal in length”.