समान जीवाएं और उनकी केंद्र से दूरीयाँ

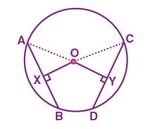
जीवा एक रेखाखंड है जो वृत्त की परिधि पर दो बिंदुओं को जोड़ता है। सामान्यतः, एक वृत्त में अनंत जीवाएँ हो सकती हैं। एक बिंदु से रेखा की दूरी को एक बिंदु से एक रेखा तक लंबवत दूरी के रूप में परिभाषित किया जाता है। यदि हम एक वृत्त पर अनंत जीवाएँ खींचते हैं, तो लंबी जीवा वृत्त के केंद्र के करीब होती है, छोटी जीवा की तुलना में। यहां हम समान जीवाओं और केंद्र से उनकी दूरी से संबंधित प्रमेय और प्रमाण तथा इसके व्युत्क्रम प्रमेय पर विस्तार से चर्चा करेंगे।

Equal Chords and their Distance from the Centre – Theorem and Proof

Theorem:

Equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres).

Proof:

Fig. 2

Consider a circle with centre $O$.

$AB$ and $CD$ are the equal chords of a circle i.e $AB=CD$

The line $OX$ is perpendicular to the chord $AB$ and $OY$ is perpendicular to the chord $CD$.

We have to prove $OX=OY$.

Also, the line $OX$ is perpendicular to $AB$.

As the perpendicular from the centre of the circle to a chord, bisects the chord, we can write it as

$AX=BX={\frac {AB}{2}}....(1)$

Similarly, the line $OY$ is perpendicular to $CD$,

$CY=DY={\frac {CD}{2}}....(2)$ [Since, the perpendicular from the centre of the circle to a chord, bisects the chord)

Given that, $AB=CD$

${\frac {AB}{2}}={\frac {CD}{2}}....(2)$

Therefore, $AX=CY....(3)$ [Using $(1)$ and $(2)$]

Now, by using the triangles $AOX$ and $COY$ ,

$\angle OXA=\angle OYC=90^{\circ }$

$OA=OC$ (Radii)

$AX=CY....(3)$

From the RHS rule, we can write it as

$\triangle AOX\cong \triangle COY$

Hence, we can conclude that $OX=OY$(Using CPCT)

Therefore, the theorem “equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres)”, is proved.

Converse of this Theorem

The converse of the above-mentioned theorem is “chords equidistant from the centre of a circle are equal in length”.