चक्रीय चतुर्भुज

चक्रीय चतुर्भुज

A cyclic quadrilateral is a four-sided polygon inscribed in a circle. It has the maximum area possible with the given side lengths. In other words, a quadrilateral inscribed in a circle depicts the maximum area possible with those side lengths.

चक्रीय चतुर्भुज की परिभाषा

A cyclic quadrilateral means a quadrilateral that is inscribed in a circle. That means there is a circle that passes through all four vertices of the quadrilateral. The vertices are said to be concyclic. The center of the circle is known as the circumcenter and the radius of the circle is known as the circumradius.

The word "cyclic" is from the Greek word "kuklos", which means "circle" or "wheel". The word "quadrilateral" is derived from the ancient Latin word "Quadri", which means "four-side" or "latus".

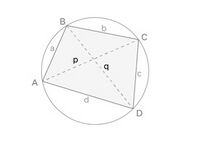
In the figure given below, $ABCD$ is a cyclic quadrilateral with $a,b,c,d$ as the side-lengths and $p,q$ as the diagonals.

Fig. 1

चक्रीय चतुर्भुज के गुणधर्म

The properties of a cyclic quadrilateral help us to identify this figure easily and to solve questions based on it. Some of the properties of a cyclic quadrilateral are given below:

• In a cyclic quadrilateral, all the four vertices of the quadrilateral lie on the circumference of the circle.
• The four sides of the inscribed quadrilateral are the four chords of the circle.
• The measure of an exterior angle at a vertex is equal to the opposite interior angle.
• In a cyclic quadrilateral, $p\times q$ = sum of product of opposite sides, where $p,q$ are the diagonals.
• The perpendicular bisectors are always concurrent.
• The perpendicular bisectors of the four sides of the cyclic quadrilateral meet at the center O.
• The sum of a pair of opposite angles is $180^{\circ }$(supplementary). Let $\angle A,\angle B,\angle C,\angle D$ be the four angles of an inscribed quadrilateral. Then, $\angle A+\angle C=180^{\circ }$ and$\angle B+\angle D=180^{\circ }$.

Theorems related to Cyclic Quadrilateral are mentioned below.

Theorem 1: The sum of either pair of opposite angles of a cyclic quadrilateral is $180^{\circ }$.

Theorem 2: If the sum of a pair of opposite angles of a quadrilateral is $180^{\circ }$, the quadrilateral is cyclic.

चक्रीय चतुर्भुज का क्षेत्रफल

The area of a cyclic quadrilateral is ${\sqrt {(s-a)(s-b)(s-c)(s-d)}}$ where $a,b,c,d$ are the four sides of the quadrilateral and $s$ is the semi perimeter which can be calculated as

$s={\frac {1}{2}}\times (a+b+c+d)$. Heron's formula for a triangle is also derived from this equation.

उदाहरण

चित्र -2

1: चित्र 2 में, $ABCD$ एक चक्रीय चतुर्भुज है जिसमें $AC$ और $BD$ इसके विकर्ण हैं।

यदि $\angle DBC=55^{\circ }$और $\angle BAC=45^{\circ }$हैं , $\angle BCD$ ज्ञात कीजिए

हल:

$\angle CAD=\angle DBC=55^{\circ }$(एक ही खंड में कोण)

अत:, $\angle DAB=\angle CAD+\angle BAC$

$\angle DAB=55^{\circ }+45^{\circ }=100^{\circ }$

परंतु $\angle DAB+\angle BCD=180^{\circ }$(चक्रीय चतुर्भुज के विपरीत कोण)

$\angle BCD=180^{\circ }-\angle DAB$

$\angle BCD=180^{\circ }-100^{\circ }=80^{\circ }$

A cyclic quadrilateral is a four-sided polygon inscribed in a circle. It has the maximum area possible with the given side lengths. In other words, a quadrilateral inscribed in a circle depicts the maximum area possible with those side lengths.

चित्र -1

एक चतुर्भुज ABCD चक्रीय कहलाता है यदि इसके चारों शीर्ष एक वृत्त पर स्थित हों (चित्र-1 देखें)।

यहाँ हमें $\angle A+\angle C=180^{\circ }$and $\angle B+\angle D=180^{\circ }$प्राप्त होता है।

चक्रीय चतुर्भुज से संबंधित प्रमेय नीचे उल्लिखित हैं।

प्रमेय 1: चक्रीय चतुर्भुज के विपरीत कोणों के किसी भी युग्म का योग $180^{\circ }$ होता है।

प्रमेय 2: यदि चतुर्भुज के विपरीत कोणों के किसी युग्म का योग $180^{\circ }$ है, तो चतुर्भुज चक्रीय होता है।