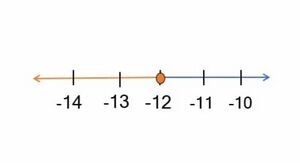एक चर राशि के रैखिक असमिकाओं का बीजगणितीय हल और उनका आलेखीय निरूपण
रैखिक असमिकाओं पर किए जाने वाले प्रकार के संक्रिया जोड़, घटाव, गुणा और भाग हैं। समान समाधान वाली रैखिक असमिकाओं को समतुल्य असमिका कहा जाता है। समानता और असमिका दोनों के लिए नियम हैं। नीचे दिए गए सभी नियम () से कम या बराबर और () से अधिक या बराबर वाली असमिकाओं के लिए भी सही हैं। रैखिक असमिकाओं को हल करने का तरीका सीखने से पहले, आइए इन सभी ऑपरेशनों के लिए असमिका के कुछ महत्वपूर्ण नियमों को देखें।
रैखिक असमिकाओं की प्रणाली को हल करना
बहु-चरणीय एक चर में रैखिक असमिकाओं को हल करना बहु-चरणीय रैखिक समीकरणों को हल करने के समान है; चर को स्थिरांक से अलग करके शुरू करें। असमानताओं के नियमों के अनुसार, जब हम बहु-चरणीय रैखिक असमानताओं को हल कर रहे होते हैं, तो हमारे लिए यह महत्वपूर्ण है कि हम ऋणात्मक संख्याओं से गुणा या भाग करते समय असमिका चिह्न को उलटना न भूलें।
चरण 1: असमिका के नियमों के अनुसार दोनों तरफ असमिकाको सरल करें - के साथ-साथ पर भी।
चरण 2: जब मान प्राप्त हो जाता है, यदि असमिका एक सख्त असमिका है, तो का हल प्रश्न में परिभाषित प्राप्त मान से कम या अधिक होता है। और, यदि असमिका एक सख्त असमिका नहीं है, तो का हल प्रश्न में परिभाषित प्राप्त मान से कम या बराबर या अधिक या बराबर होता है।
अब, अवधारणा को समझने के लिए, एक उदाहरण के साथ रैखिक असमिकाओं को हल करने का प्रयास करें।
इस रैखिक असमिका को हल करने के लिए, हम नीचे दिए गए चरणों का पालन करेंगे:
इस असमिका का समाधान के उन सभी मानों का समूह होगा जिनके लिए यह असमिका संतुष्ट है, यानी से सख्ती से बड़ी सभी वास्तविक संख्याएँ।
दोनों पक्षों पर चर के साथ रैखिक असमानताओं को हल करना
आइए हम सीखी गई अवधारणा को लागू करके एक चर के साथ रैखिक असमिकाओं को हल करने का प्रयास करें। निम्नलिखित उदाहरण पर विचार करें।
हम इस प्रकार आगे बढ़ते हैं:
रैखिक असमिकाओं की प्रणाली को रेखांकन द्वारा हल करना
दो-चर रैखिक असमिकाओं की प्रणाली या के रूप की होती है। असमिकाओं के चिह्न दिए गए असमिकाओं के समूह के अनुसार बदल सकते हैं। दो-चर रैखिक असमिकाओं की प्रणाली को हल करने के लिए, हमारे पास कम से कम दो असमानताएँ होनी चाहिए। अब, दो चरों में रैखिक असमिकाओं की प्रणाली को हल करने के लिए, आइए एक उदाहरण पर विचार करें।
और
सबसे पहले, हम दी गई असमिकाओं को ग्राफ पर अंकित करेंगे। ऐसा करने के लिए, दिए गए चरणों का पालन करें:
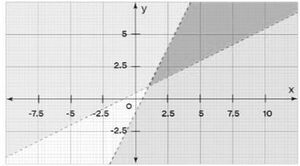
असमिका चिह्न को = के बराबर से बदलें, अर्थात, हमारे पास और है। चूँकि रैखिक असमिका सख्त है, इसलिए हम ग्राफ पर बिंदीदार रेखाएँ खींचते हैं।
जाँचें कि क्या मूल बिंदु दी गई रैखिक असमिकाओं को संतुष्ट करता है। यदि ऐसा है, तो उस रेखा के एक तरफ के क्षेत्र को छायांकित करें जिसमें मूल बिंदु उपस्थित है। यदि मूल बिंदु रैखिक असमिका को संतुष्ट नहीं करता है, तो उस रेखा के एक तरफ के क्षेत्र को छायांकित करें जिसमें मूल बिंदु उपस्थित नहीं है।
के लिए, को प्रतिस्थापित करें, हमारे पास है: जो सत्य नहीं है। इसलिए, रेखा के उस पक्ष को छायांकित करें जिसमें मूल बिंदु उपस्थित नहीं है। इसी तरह, के लिए, प्रतिस्थापित करने पर, हमारे पास है: जो सत्य नहीं है। इसलिए, रेखा की भुजा है जिसमें मूल उपस्थित नहीं है।
उभयनिष्ठ छायांकित वह संभव क्षेत्र होगा जो रैखिक असमिकाओं की प्रणाली का समाधान बनाता है। यदि कोई उभयनिष्ठ छायांकित क्षेत्र नहीं है, तो समाधान मौजूद नहीं है। नीचे दिए गए ग्राफ में बैंगनी रंग का क्षेत्र रैखिक असमिकाओं की दी गई प्रणाली का समाधान दिखाता है।
रैखिक असमिकाओं का आलेखीय निरूपण
एक चर वाली रैखिक असमिकाओं को संख्या रेखा पर प्लॉट किया जाता है, क्योंकि आउटपुट एक चर का हल देता है। इसलिए, एक चर वाली रैखिक असमिकाओं का ग्राफ़ केवल संख्या रेखा का उपयोग करके किया जाता है। इसके विपरीत, दो चर वाली रैखिक असमिकाओं को दो-आयामी और अक्ष ग्राफ़ पर आलेख किया जाता है, क्योंकि आउटपुट दो चर का हल देता है। इसलिए, दो-चर वाली रैखिक असमिकाओं का ग्राफ़, ग्राफ़ का उपयोग करके किया जाता है।
रैखिक असमिकाओं का आलेखीय निरूपण - एक चर
आइए नीचे दिए गए उदाहरण पर विचार करें।
इस मामले में समाधान सरल है।
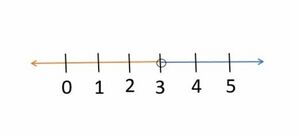
इसे संख्या रेखा पर इस प्रकार दर्शाया जा सकता है:
संख्या रेखा के नीले भाग पर स्थित कोई भी बिंदु इस असमिका को संतुष्ट करेगा। ध्यान दें कि इस मामले में, हमने बिंदु 3 पर एक खोखला बिंदु बनाया है। यह इंगित करने के लिए है कि 3 समाधान समुच्चय का भाग नहीं है (ऐसा इसलिए है क्योंकि दी गई असमिकामें सख्त असमिकाहै)। प्राप्त समाधान के अनुसार, संख्या रेखा का नीला भाग असमिका को संतुष्ट करता है। आइए रैखिक असमानताओं का एक और उदाहरण लेते हैं:
हम इस प्रकार आगे बढ़ते हैं:
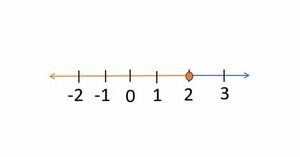
हम इस समाधान समुच्चय को एक संख्या रेखा पर दर्शाना चाहते हैं। इस प्रकार, हम संख्या रेखा के उस भाग को चिन्हांकित करते हैं जो 2 के बाईं ओर स्थित है
हम देखते हैं कि संख्या रेखा के लाल भाग पर स्थित कोई भी संख्या इस असमिका को संतुष्ट करेगी और इसलिए यह इस असमिका के लिए समाधान समुच्चय का एक भाग है। ध्यान दें कि हमने बिंदु 2 पर बिल्कुल एक ठोस बिंदु खींचा है। यह इंगित करता है कि 2 भी समाधान समुच्चय का एक भाग है।
उदाहरण
उदाहरण 1. रैखिक असमिका, का हल ज्ञात करें और इसे संख्या रेखा पर अंकित करें।
समाधान: हम समस्या को निम्न प्रकार से हल करेंगे:
रैखिक असमिका को निम्न प्रकार से संख्या रेखा पर अंकित किया जाएगा:
समाधान समुच्चय ऊपर प्लॉट किया गया है। हम कह सकते हैं कि संख्या रेखा के लाल भाग पर स्थित कोई भी संख्या इस रैखिक असमानता को संतुष्ट करेगी और इसलिए यह इस असमानता के समाधान समुच्चय का एक भाग है। इसलिए, हमने बिंदु -12 पर बिल्कुल एक ठोस बिंदु खींचा है। यह इंगित करना है कि -12 भी समाधान समुच्चय का एक भाग है।
उत्तर: इसलिए, समाधान है