एक बिंदु से एक वृत्त पर स्पर्श रेखाओं की संख्या

गणित में, हम जानते हैं कि वृत्त एक बंद द्वि-आयामी आकृति है, जिसमें वृत्त की सतह पर सभी बिंदु केंद्र बिंदु से समान दूरी पर होते हैं जिसे त्रिज्या कहा जाता है। वृत्त की स्पर्शरेखा वह रेखा होती है जो वृत्त को केवल एक बिंदु पर प्रतिक्षेद करती है। वह बिंदु जहाँ वृत्त और स्पर्शरेखा स्पर्श करते हैं उसे संपर्क बिंदु कहा जाता है। हम वृत्त पर एक बिंदु से स्पर्शरेखाओं की संख्या के लिए तीन अलग-अलग मामले देख सकते हैं।

स्तिथि 1: कोई स्पर्शरेखा नहीं

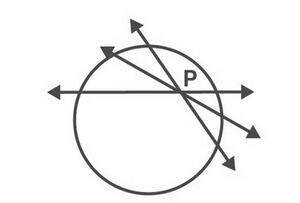
वृत्त के अंदर स्थित किसी बिंदु से होकर गुजरने वाली वृत्त की कोई स्पर्श रेखा नहीं होती।

चित्र-1

स्तिथि 2: एक स्पर्शरेखा

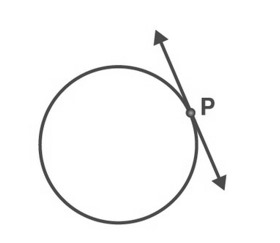
वृत्त पर स्थित एक बिंदु से होकर गुजरने वाली वृत्त की एक ही स्पर्श रेखा होती है।

चित्र-2

स्तिथि 3: दो स्पर्शरेखाएँ

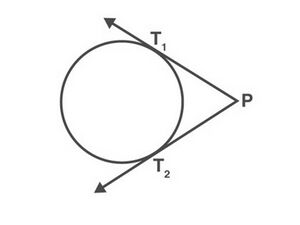
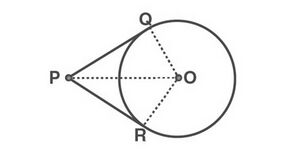
एक वृत्त पर ठीक दो स्पर्श रेखाएं होती हैं जो वृत्त के बाहर स्थित एक बिंदु से होकर गुजरती हैं।

चित्र-3

इस मामले में देखी गई दो स्पर्शरेखाएँ $PT_{1}$ और $PT_{2}$ हैं और $T_{1}$ और $T_{2}$ क्रमशः स्पर्शरेखाओं $PT_{1}$ और $PT_{2}$ के संपर्क बिंदु हैं। बिंदु 𝑃 से वृत्त पर स्पर्शरेखा की लंबाई बाहरी बिंदु $P$ से वृत्त पर संपर्क बिंदु तक स्पर्शरेखा के खंड की लंबाई है।

बिंदु से एक वृत्त पर स्पर्श रेखाओं की संख्या- प्रमेय एवं प्रमाण

वृत्त पर एक बिंदु से स्पर्शरेखाओं की संख्या से संबंधित दो प्रमेयों को विस्तार से समझाया गया है।

प्रमेय 1 :

किसी वृत्त के किसी भी बिंदु पर स्पर्श रेखा, संपर्क बिंदु से होकर जाने वाली त्रिज्या पर लंबवत होती है।

प्रमाण:

चित्र-4

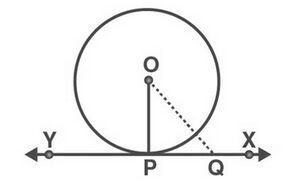
चित्र-4 पर विचार करें, जिसका केंद्र $O$ है और $XY$ संपर्क बिंदु $P$ वाले वृत्त की स्पर्श रेखा है।

प्रमाणित करने के लिए : $OP$ , $XY$ पर लंबवत है

स्पर्शरेखा $XY$ पर बिंदु $P$ के अतिरिक्त एक बिंदु $Q$ लीजिए। अब, बिंदुओं $O$ और $Q$ को मिलाइए।

ध्यान दें कि बिंदु $Q$ वृत्त के बाहर स्थित होना चाहिए। क्योंकि, यदि बिंदु $Q$ वृत्त के अंदर है, तो $XY$ एक छेदक रेखा बन जाएगी और वृत्त पर कोई स्पर्श रेखा नहीं होगी।

इसलिए, हम कह सकते हैं कि $OQ$ , $OP$ से बड़ा है।

(अर्थात) $OQ>OP$

चूँकि बिंदु वृत्त के बाहर स्थित है, इसलिए उपरोक्त शर्त $XY$ पर स्थित प्रत्येक बिंदु के लिए लागू है, बिंदु $P$ को छोड़कर।

इस प्रकार, $OP$ बिंदु $O$ की स्पर्श रेखा $XY$ पर स्थित बिंदुओं से न्यूनतम दूरी है।

इसलिए, $OP$ स्पर्शरेखा $XY$ पर लंबवत है।

प्रमेय 2:

किसी बाह्य बिंदु से वृत्त पर खींची गई स्पर्श रेखाओं की लंबाइयाँ समान होती हैं।

प्रमाण:

चित्र-5

चित्र-5 में दिए गए वृत्त पर विचार करें जिसका केंद्र $O$ है और $P$ वह बिंदु है जो वृत्त के बाहर स्थित है। अतः, बनने वाली दो स्पर्शरेखाएँ $PQ$ और $PR$ हैं।