कोण-कोण-कोण समरूपता कसौटी

त्रिभुजों की समरूपता के लिए कोण-कोण-कोण (AAA) कसौटी/मानदंड बताता है कि "यदि दो त्रिभुजों में संगत कोण समान हैं, तो उनकी संगत भुजाएँ समान अनुपात (या समानुपात) में होती हैं और इसलिए दोनों त्रिभुज समरूप होते हैं"।

प्रमाण:

चित्र-1

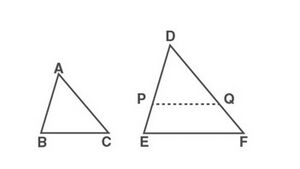
दो त्रिभुजों $ABC$ और $DEF$ पर विचार करें जैसे कि $\angle A=\angle D$, $\angle B=\angle E$, $\angle C=\angle F$ जैसा कि चित्र-1 में दर्शाया गया है।

अब, $DP=AB$ और $DQ=AC$ को विभाजित करें/काटें और $PQ$ को मिलाएँ। इसलिए, हम कह सकते हैं कि एक त्रिभुज $ABC$ त्रिभुज $DPQ$ के सर्वांगसम है।(अर्थात) $\triangle ABC\cong \triangle DPQ$ जो $\angle B=\angle P=\angle E$ और साथ ही, रेखा $PQ\parallel EF$ देता है।

इसलिए, मूल आनुपातिकता प्रमेय का उपयोग करके, हम निम्नलिखित प्रकार से लिख सकते हैं

${\frac {DP}{PE}}={\frac {DQ}{QF}}$

${\frac {AB}{DE}}={\frac {AC}{DF}}....(1)$

इसी तरह

${\frac {AB}{DE}}={\frac {BC}{EF}}....(2)$

$(1)(2)$ से हम लिख सकते हैं

${\frac {AB}{DE}}={\frac {BC}{EF}}={\frac {AC}{DF}}....(1)$

अतः दोनों त्रिभुज ABC और DEF समरूप हैं।

उदाहरण

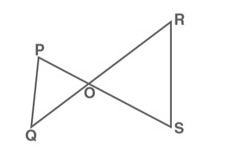
1.दर्शाइए कि त्रिभुज $POQ$ तथा $SOR$ समरूप त्रिभुज हैं, यह देखते हुए कि $PQ$, $RS$ के समानान्तर है जैसा कि नीचे दिए गए चित्र में दिखाया गया है।

हल:

मान लें कि $PQ$, $RS$ के समानांतर है (अर्थात) $PQ\parallel RS$

वैकल्पिक कोण गुण का उपयोग करके, $\angle P=\angle S$ और $\angle Q=\angle R$

साथ ही, शीर्षाभिमुख कोणों का उपयोग करके, $\angle POQ=\angle SOR$

इसलिए, हम यह निष्कर्ष निकाल सकते हैं कि त्रिभुज $POQ$ त्रिभुज $SOR$ के समरूप है

(अर्थात) $\triangle POQ\sim \triangle SOR$ (त्रिभुजों के लिए AAA समरूप/ता कसौटीमानदंड का उपयोग करके)

अतः सिद्ध हुआ।