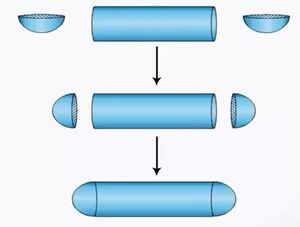
ठोसों के संयोजन का पृष्ठीय क्षेत्रफल

चित्र-1 - ठोसों के संयोजन का पृष्ठीय क्षेत्रफल

आइए चित्र-1 में दिखाए गए कंटेनर पर विचार करें। हम ऐसे ठोस का पृष्ठीय क्षेत्रफल कैसे ज्ञात करेंगे? यह ठोस एक बेलन से बना है जिसके दोनों सिरों पर दो अर्धगोले लगे हुए हैं।

नये ठोस का कुल पृष्ठीय क्षेत्रफल (TSA) = एक गोलार्ध का वक्र पृष्ठीय क्षेत्रफल (CSA) +

बेलन का वक्रीय सतही क्षेत्रफल (CSA) + अन्य गोलार्धों का वक्रीय सतही क्षेत्रफल (CSA)।

गोलार्ध का वक्र पृष्ठीय क्षेत्रफल (CSA) =$2\Pi r^{2}$

बेलन का वक्र पृष्ठीय क्षेत्रफल (CSA) =$2\Pi rh$

उदाहरण

1. एक ठोस बेलन के प्रत्येक सिरे से एक अर्धगोला निकालकर लकड़ी की एक वस्तु बनाई गई, यदि बेलन की ऊंचाई 10 सेमी है, और इसका आधार त्रिज्या 3.5 सेमी है,वस्तु का कुल पृष्ठीय क्षेत्रफल ज्ञात करें।

हल:

यहाँ $h=10,r=3.5$

लकड़ी के सामान का कुल पृष्ठीय क्षेत्रफल (TSA) = बेलन का वक्र पृष्ठीय क्षेत्रफल (CSA) + 2 x अर्धगोले का वक्र पृष्ठीय क्षेत्रफल (CSA)

$=2\Pi rh+2\times 2\Pi r^{2}$

$=2\times {\frac {22}{7}}\times 3.5\times 10+2\times 2\times {\frac {22}{7}}\times 3.5^{2}$

$=220+154=374$ cm²

वस्तु का कुल पृष्ठीय क्षेत्रफल $374$ cm² है।

चित्र. 2

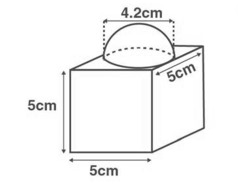
2. जैसा कि चित्र में दिखाया गया है, एक ब्लॉक दो ठोस पदार्थों जैसे घन और अर्धगोले से बना है। ब्लॉक(खंड) का आधार एक घन है जिसका कोर/किनारा $5$ cm है और शीर्ष पर लगे अर्धगोले का व्यास $4.2$ cm है । ब्लॉक का कुल पृष्ठीय क्षेत्रफल ज्ञात करें ($\pi ={\frac {22}{7}}$ लें)

हल:

दिया गया है: घन का किनारा $a=5$ cm

घन का कुल पृष्ठीय क्षेत्रफल = $6a^{2}$वर्ग इकाई

घन का TSA = $6\times 5^{2}=6\times 25=150\ cm^{2}$

दी गई आकृति से, यह देखा जा सकता है कि एक अर्धगोला घन के भाग से जुड़ा हुआ है।

इसलिए घन का भाग पृष्ठीय क्षेत्रफल में उपस्थित नहीं है।

ब्लॉक का पृष्ठीय क्षेत्रफल = घन का TSA - गोलार्ध का आधार क्षेत्रफल + गोलार्ध का CSA

ब्लॉक का पृष्ठीय क्षेत्रफल = $150-\pi r^{2}+2\pi r^{2}cm^{2}$

ब्लॉक का पृष्ठीय क्षेत्रफल = $150+\pi r^{2}cm^{2}$

ब्लॉक का पृष्ठीय क्षेत्रफल = $150+{\frac {22}{7}}\times (2.1)^{2}cm^{2}$

ब्लॉक का पृष्ठीय क्षेत्रफल = $150+13.86\ cm^{2}=163.86\ cm^{2}$

अतः ब्लॉक का पृष्ठीय क्षेत्रफल $163.86\ cm^{2}$ है।