त्रिभुजों की सर्वांगसमता के लिए कसौटीयाँ
त्रिभुजों की सर्वांगसमता में कहा गया है कि दो त्रिभुज सर्वांगसम कहलाते हैं यदि वे एक-दूसरे की प्रतिलिपियाँ हों और जब एक दूसरे पर अध्यारोपित हों, तो वे एक-दूसरे को बिल्कुल समाविष्ट करती हैं। अन्य शब्दों में, यदि त्रिभुज की भुजाएँ और कोण दूसरे त्रिभुज की संगत भुजाओं और कोणों के समान हों तो दो त्रिभुज सर्वांगसम होते हैं।
त्रिभुजों की सर्वांगसमता के मानदंड नीचे समझाये गये हैं।
अभिगृहीत 1 SAS (भुजा-कोण-भुजा) सर्वांगसमता नियम: दो त्रिभुज सर्वांगसम होते हैं यदि एक त्रिभुज की दो भुजाएँ और सम्मिलित कोण दूसरे त्रिभुज की दो भुजाओं और सम्मिलित कोण के समान हों।
प्रमाण:
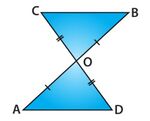
दिए गए चित्र में और .
यह बताओ की
(i) और (ii) .
हल:
दिए गए आंकड़े: और त्रिभुज में. और
(शीर्षाभिमुख कोण)
अत: (SAS सर्वांगसमता नियम का उपयोग करना)
(ii) सर्वांगसम त्रिभुजों और में, त्रिभुज की भुजाओं के संगत भाग भी समान होते हैं।
अत: और ये स्थितियाँ रेखाखंडों और के लिए वैकल्पिक कोणों की एक जोड़ी बनाती हैं।
इसलिए भुजाएँ ।
अतः सिद्ध हुआ। प्रमेय 1 (ASA सर्वांगसमता नियम): दो त्रिभुज सर्वांगसम होते हैं यदि एक त्रिभुज के दो कोण और सम्मिलित भुजा अन्य त्रिभुजों के दो कोणों और सम्मिलित भुजा के समान हों।
प्रमेय 1 ASA (कोण-भुजा-कोण) सर्वांगसमता नियम: दो त्रिभुज सर्वांगसम होते हैं यदि एक त्रिभुज के दो कोण और सम्मिलित भुजा दूसरे त्रिभुज के दो कोणों और सम्मिलित भुजा के समान हों।
प्रमाण:
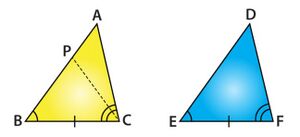
दिए गए दो त्रिभुजों और में से, जिसमें:
और और
यह सिद्ध करने के लिए
दो त्रिभुजों की सर्वांगसमता सिद्ध करने के लिए निम्नलिखित तीन स्थितियाँ सम्मिलित हैं
स्थिति (i): मान लें
यहाँ (मान लिया गया)
दिया हुआ और
तो, SAS नियम से हमें प्राप्त होता है,
स्थिति (ii): मान लीजिए की भुजा ।अब पर एक बिंदु इस प्रकार लीजिए कि वह बन जाए
अब त्रिभुजों और पर विचार करें
संरचना से,
दिया हुआ
इसलिए, SAS सर्वांगसमता स्वयंसिद्ध से हम निष्कर्ष निकालते हैं कि
चूँकि त्रिभुज सर्वांगसम हैं, अतः त्रिभुजों के संगत भाग भी समान हैं।
इसलिए,
लेकिन, हमें वह उपलब्ध कराया गया है
तो, हम कह सकते हैं
क्या ऐसा प्रतिबंध संभव है?
यह प्रतिबंध/स्थिति तभी संभव है जब 𝐴 के अनुरूप होता है या जब
इसलिए, (SAS अभिगृहीत से)
स्थिति (iii): If , हम पर एक बिंदु इस तरह ले सकते हैं कि यह बन जाए और
स्थिति (ii) में दिए गए तर्कों को दोहराते हुए, हम यह निष्कर्ष निकाल सकते हैं कि और इसलिए हमें मिलता है
AAS (कोण-कोण-भुजा) सर्वांगसमता नियम: दो त्रिभुज सर्वांगसम होते हैं यदि कोणों के कोई दो युग्म और संगत भुजाओं का एक जोड़ा समान हो।