त्रिभुज का क्षेत्रफल - सारणिक

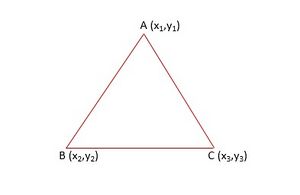
सारणिक रूप में एक त्रिभुज के क्षेत्रफल की गणना निर्देशांक ज्यामिति में की जाती है जब त्रिभुज के शीर्षों के निर्देशांक दिए जाते हैं। सारणिक के रूप में त्रिभुज का क्षेत्रफल ज्ञात करना सारणिक के महत्वपूर्ण अनुप्रयोगों में से एक है।

एक त्रिभुज का क्षेत्रफल, त्रिभुज के आधार और ऊंचाई के गुणनफल का आधा होता है। लेकिन यदि त्रिभुज की ऊंचाई अज्ञात है और उसके शीर्ष दिए गए हैं, तो हम सारणिक सूत्र का उपयोग करके त्रिभुज का क्षेत्रफल ज्ञात कर सकते हैं।

इस लेख में, हम एक त्रिभुज के क्षेत्रफल की गणना उसके सूत्र का उपयोग करके सारणिक रूप में करेंगे।

त्रिभुज - सारणिक

त्रिभुज का क्षेत्रफल

सारणिक रूप में त्रिभुज के क्षेत्रफल की गणना तब की जा सकती है जब त्रिभुज के शीर्ष दिए गए हों। शीर्ष $A(x_{1},y_{1})$, $B(x_{2},y_{2})$, $C(x_{3},y_{3})$ वाले त्रिभुज $ABC$ पर विचार करें तो यह है क्षेत्रफल की गणना इस प्रकार की जा सकती है

${\frac {1}{2}}\left[x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})\right]$

सारणिक रूप में यह व्यंजक इस प्रकार लिखी जाती है

$\bigtriangleup ={\frac {1}{2}}{\begin{vmatrix}x_{1}&y_{1}&1\\x_{2}&y_{2}&1\\x_{3}&y_{3}&1\end{vmatrix}}..............(1)$

$\bigtriangleup ={\frac {1}{2}}\left[x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})\right]$

• चूँकि क्षेत्रफल एक धनात्मक मात्रा है, हम सदैव सारणिक का निरपेक्ष मान (1) में लेते हैं।
• यदि क्षेत्रफल दिया गया है, तो गणना के लिए सारणिक के सकारात्मक और नकारात्मक दोनों मानों का उपयोग करें।
• तीन संरेख बिंदुओं से निर्मित त्रिभुज का क्षेत्रफल शून्य है

उदाहरण

उस त्रिभुज का क्षेत्रफल ज्ञात करें जिसके शीर्ष $(3,8)$, $(-4,2)$, $(5,1)$ हैं ,

त्रिभुज का क्षेत्रफल है

$\bigtriangleup ={\frac {1}{2}}{\begin{vmatrix}3&8&1\\-4&2&1\\5&1&1\end{vmatrix}}$

$\bigtriangleup ={\frac {1}{2}}\left[3(2-1)-8(-4-5)+1(-4-10)\right]$

$\bigtriangleup ={\frac {1}{2}}\left[3(1)-8(-9)+1(-14)\right]$

$\bigtriangleup ={\frac {1}{2}}\left[3+72-14\right]$

$\bigtriangleup ={\frac {1}{2}}\left[61\right]$

$\bigtriangleup ={\frac {61}{2}}$