पाइथागोरस प्रमेय

पाइथागोरस प्रमेय गणित का एक महत्वपूर्ण विषय है, जो समकोण त्रिभुज की भुजाओं के बीच के संबंध को बताता है।

पाइथागोरस प्रमेय का उपयोग मूल रूप से किसी त्रिभुज की अज्ञात भुजा की लंबाई और कोण ज्ञात करने के लिए किया जाता है। इस प्रमेय के द्वारा हम आधार, लम्ब और कर्ण सूत्र प्राप्त कर सकते हैं।

पाइथागोरस प्रमेय कथन

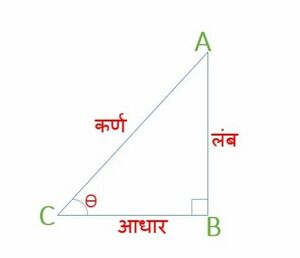
पाइथागोरस प्रमेय कहता है कि "एक समकोण त्रिभुज में, कर्ण भुजा का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर होता है"। इस त्रिभुज की भुजाओं को लंब, आधार और कर्ण नाम दिया गया है। यहां, कर्ण सबसे लंबी भुजा है, क्योंकि यह कोण 90° के विपरीत है।

चित्र में $ABC$ जहां भुजा $AB$ को लंब कहा जाता है, भुजा $BC$ को आधार कहा जाता है, भुजा $AC$ को कर्ण कहा जाता है।