भुजा- भुजा- भुजा समरूपता कसौटी

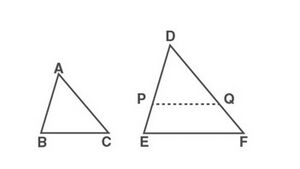
दो त्रिभुजों की समरूपता के लिए भुजा- भुजा- भुजा (SSS) कसौटी/मानदंड बताता है कि "यदि दो त्रिभुजों में, एक त्रिभुज की भुजाएँ दूसरे त्रिभुज की भुजाओं के समानुपाती (अर्थात्, उसी अनुपात में) हैं, तो उनके संगत कोण समान हैं और इसलिए दोनों त्रिभुज समरूप हैं”।

चित्र-1

प्रमाण:

चित्र-1 पर विचार करें। यह देखा गया है कि ${\frac {DP}{PE}}={\frac {DQ}{QF}}$ और त्रिभुज $DEF$ में भी, रेखा $PQ$ रेखा $EF$ के समानांतर है।

इसलिए, $\angle P=\angle E$ और $\angle Q=\angle F$

अत: हम लिख सकते हैं: ${\frac {DP}{DE}}={\frac {DQ}{DF}}={\frac {PQ}{EF}}$

उपरोक्त अभिव्यक्ति को इस प्रकार लिखा गया है

${\frac {DP}{DE}}={\frac {DQ}{DF}}={\frac {BC}{EF}}$

इसका मतलब यह है कि $PQ=BC$.

अतः त्रिभुज $ABC$, $DPQ$ त्रिभुज के सर्वांगसम है (अर्थात्) $\triangle ABC\cong \triangle DPQ$

इस प्रकार, त्रिभुज की समरूपता के लिए AAA मानदंड का उपयोग करके, हम कह सकते हैं कि

$\angle A=\angle D$ , $\angle B=\angle E$ , $\angle C=\angle F$

उदाहरण

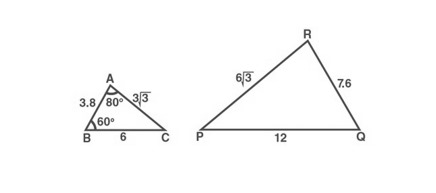
1.निम्नलिखित त्रिभुजों में $\angle P$ ज्ञात कीजिए।

दिए गए त्रिभुजों $ABC$ और $PQR$ से, हम प्राप्त कर सकते हैं

${\frac {AB}{RQ}}={\frac {3.8}{7.6}}={\frac {1}{2}}$

${\frac {BC}{QP}}={\frac {6}{12}}={\frac {1}{2}}$

${\frac {CA}{PR}}={\frac {3{\sqrt {3}}}{6{\sqrt {3}}}}={\frac {1}{2}}$

अतः,

${\frac {AB}{RQ}}={\frac {BC}{QP}}={\frac {CA}{PR}}$

इसलिए, एक त्रिभुज के लिए SSS समरूपता कसौटी/मानदंड का उपयोग करके, हम लिख सकते हैं

$\triangle ABC\sim \triangle RQP$ (अर्थात्) $\triangle ABC$ ,$\triangle RQP$ के समान/समरूप है

समरूप त्रिभुजों के संगत कोणों का उपयोग करके,

$\angle C=\angle P$

$\angle C=180^{\circ }-\angle A-\angle B$

$\angle C=180^{\circ }-80^{\circ }-60^{\circ }$

$\angle C=40^{\circ }$

इसलिए $\angle C=\angle P$, का मान $\angle P=40^{\circ }$ है