रेखा का व्यापक समीकरण
एक सरल रेखा का व्यापक समीकरण है, जहाँ रेखा की ढाल है और -अंत: खंड है। यह एक सरल रेखा के समीकरण का सबसे व्यापक रूप है जिसका उपयोग ज्यामिति में किया जाता है। एक सरल रेखा के समीकरण को विभिन्न रूपों में लिखा जा सकता है जैसे बिंदु-की ढाल रूप, ढाल-अंत: खंड रूप, अंत: खंड रूप, मानक रूप, आदि। एक सरल रेखा एक द्वि-आयामी ज्यामितीय इकाई है जो अनंत तक दोनों सिरों पर फैली हुई है।
इस लेख में, हम एक सरल रेखा के समीकरण की अवधारणा को विभिन्न रूपों में समझेंगे।
परिभाषा
एक सरल रेखा का समीकरण दो चर (साधारणतः और ) में एक रैखिक समीकरण है और रेखा पर प्रत्येक बिंदु द्वारा संतुष्ट होता है। यानी यह एक गणितीय समीकरण है जो उस सरल रेखा पर स्थित निर्देशांक बिंदुओं के बीच संबंध देता है। इसे विभिन्न रूपों में लिखा जा सकता है और यह रेखा की ढाल, -अंत: खंड और -अंत: खंड को बताता है। इसका उपयोग रेखा पर बिंदुओं को ज्ञात करने के लिए भी किया जा सकता है। अधिकतर, सरल रेखा का समीकरण बिंदु-ढलान रूप, ढलान-अंत: खंड रूप, दो-बिंदु रूप, मानक रूप आदि का उपयोग करके पाया जाता है। आइए सरल रेखा के समीकरण के सूत्र के माध्यम से चलते हैं। सरल रेखा का समीकरण ज्ञात करने के लिए सबसे आम सूत्र नीचे दिए गए हैं।
सरल रेखा के समीकरण सूत्र
सरल रेखा के समीकरण सूत्र रेखा के बारे में उपलब्ध जानकारी जैसे रेखा की ढाल, अंत: खंड आदि के आधार पर भिन्न होते हैं। ध्यान दें कि दो बिंदुओं और वाली रेखा के ढलान की गणना सूत्र द्वारा की जाती है। यहाँ अलग-अलग सरल रेखा सूत्र दिए गए हैं।
रेखा के समीकरण के रूप
सरल रेखा के लिए ज्ञात मापदंडों के आधार पर, रेखा के समीकरण के 5 रूप हैं जिनका उपयोग रेखा के समीकरण को निर्धारित करने और उसका प्रतिनिधित्व करने के लिए किया जाता है:
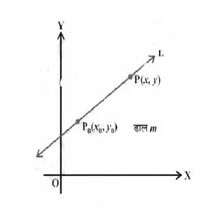
बिंदु ढाल रूप –
इस रूप में रेखा पर एक बिंदु और रेखा की ढलान की आवश्यकता होती है। रेखा पर संदर्भित बिंदु है और रेखा की ढलान है। बिंदु एक संख्यात्मक मान है और बिंदु के -निर्देशांक और -निर्देशांक को दर्शाता है और रेखा की ढलान सकारात्मक -अक्ष के साथ एक रेखा का झुकाव है।
यहाँ, में सकारात्मक, नकारात्मक या शून्य ढलान हो सकता है। इसलिए, एक रेखा का समीकरण इस प्रकार है:
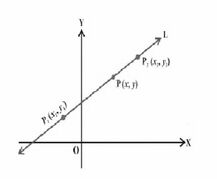
दो बिंदु रूप –
यह रूप दो बिंदुओं -और से होकर गुजरने वाली रेखा के बिंदु-ढलान का एक और स्पष्टीकरण है:
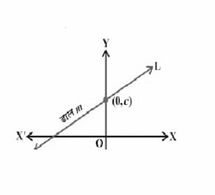
ढाल अंत: खंड रूप –
रेखा का ढलान-अंत: खंड रूप है। यहाँ, '' रेखा का ढलान है, और '' रेखा का -अंत: खंड है। यह रेखा -अक्ष को बिंदु पर काटती है, जहाँ मूल बिंदु से -अक्ष पर इस बिंदु की दूरी है।
ढलान-अंत: खंड रूप एक महत्वपूर्ण रूप है और गणित के विभिन्न विषयों में इसके बहुत अच्छे अनुप्रयोग हैं।
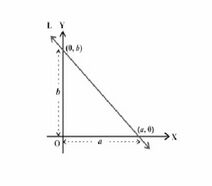
अंत: खंड रूप –
इस रूप में रेखा का समीकरण -अंत: खंड और -अंत: खंड से बनता है। रेखा -अक्ष को एक बिंदु पर काटती है, और -अक्ष को एक बिंदु पर काटती है, और मूल बिंदु से इन बिंदुओं की क्रमशः दूरी है। जबकि इन दो बिंदुओं को दो-बिंदु रूप में प्रतिस्थापित किया जा सकता है और रेखा के समीकरण के इस अंत: खंड रूप को प्राप्त करने के लिए सरलीकृत किया जा सकता है।
रेखा के समीकरण का अंत: खंड रूप उस दूरी को स्पष्ट करता है जिस पर रेखा -अक्ष और -अक्ष को मूल बिंदु से काटती है।
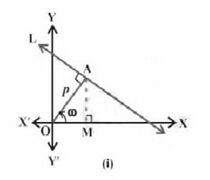
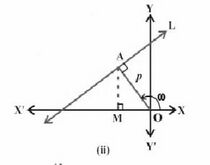
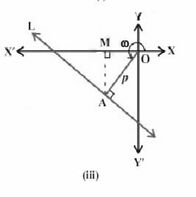
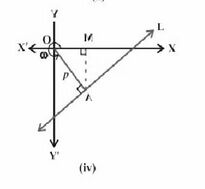
लंब रूप -
लंब रूप दी गई रेखा के लंबवत रेखा पर आधारित होता है, जो मूल बिंदु से होकर गुजरती है,
और इसे लंब के रूप में जाना जाता है।
यहाँ, लंब की लंबाई के पैरामीटर '' हैं और इस लंब द्वारा धनात्मक -अक्ष के साथ बनाया गया कोण '' है जो एक रेखा के समीकरण को बनाने के लिए उपयोगी है। रेखा के समीकरण का लंब रूप इस प्रकार है:
(i) मूल बिंदु से रेखा पर लंब की लंबाई।
(ii) लंब एवं धन -अक्ष के बीच का कोण।
आलेख पर सरल रेखा का समीकरण
एक चर में रैखिक समीकरण का ग्राफ -अक्ष के समानांतर एक ऊर्ध्वाधर रेखा बनाता है और एक चर में सरल रेखा के समीकरण का ग्राफ -अक्ष के समानांतर एक क्षैतिज रेखा है। दो चर और में रैखिक समीकरण का ग्राफ कुछ ढलान के साथ एक सरल रेखा बनाता है।
यदि एक सरल रेखा बाएं से दाएं बढ़ रही है, तो इसका ढलान धनात्मक है। यदि यह घट रही है, तो इसका ढलान ऋणात्मक है।
महत्वपूर्ण टिप्पणियाँ
- एक सरल रेखा के समीकरण को दो चरों में रैखिक समीकरण भी कहा जाता है।
- यदि दो सरल रेखाओं के ढलानों का गुणनफल है, तो रेखाएँ एक दूसरे के लंबवत हैं।
- यदि दो सरल रेखाएँ एक दूसरे के समानांतर हैं, तो उनका ढलान समान होगा।
- बिंदु ढलान रूप:
- ढलान-अवरोधन रूप:
- मानक रूप