एक बिंदु किसी रेखाखंड पर उसे दो भागों में विभाजित करता है, जो समान या असमान हो सकते हैं। यदि हमें उस बिंदु के निर्देशांक ज्ञात हैं, तो हम उस अनुपात का निर्धारण कर सकते हैं जिसमें वह बिंदु रेखाखंड को विभाजित करता है। इसी प्रकार, यदि रेखाखंड को विभाजित करने का अनुपात ज्ञात हो, तो विभाजन बिंदु के निर्देशांक भी प्राप्त किए जा सकते हैं। निर्देशांक ज्यामिति में यह कार्य अनुभाग सूत्र की सहायता से किया जाता है, जो इन दोनों स्थितियों में उपयोगी है।
अनुभाग सूत्र का उपयोग उस बिंदु के निर्देशांक निर्धारित करने के लिए किया जाता है जो दो बिंदुओं को जोड़कर एक रेखाखंड को दो भागों में विभाजित करता है, जैसे कि उनकी लंबाई का अनुपात  है।
है।
मान लीजिए  और
और  क्रमशः दो बिंदु
क्रमशः दो बिंदु  और
और  हैं, और
हैं, और  वह बिंदु है जो रेखाखंड
वह बिंदु है जो रेखाखंड  को
को  के अनुपात में आंतरिक रूप से विभाजित करता है, तो बिंदु
के अनुपात में आंतरिक रूप से विभाजित करता है, तो बिंदु  के निर्देशांक निर्धारित करने के लिए अनुभागीय सूत्र बनाएं जो इस प्रकार दिया गया है:
के निर्देशांक निर्धारित करने के लिए अनुभागीय सूत्र बनाएं जो इस प्रकार दिया गया है:

द्विविमीय ज्यामिति में हमने सीखा है कि किस प्रकार समकोणिक कार्टेशियन पद्धति में एक रेखा खंड को दिए अनुपात में अंत: विभाजित करने वाले बिंदु के निर्देशांक ज्ञात करते हैं।
अब हम इस संकल्पना का विस्तार त्रिविमीय ज्यामिति के लिए करते हैं।
मान लीजिए अंतरिक्ष में दो बिंदु  व
व  हैं। माना
हैं। माना  रेखा खंड
रेखा खंड  को
को  अनुपात में अंत: विभाजित करता है।
अनुपात में अंत: विभाजित करता है।  - तल पर
- तल पर  ,
,  और
और  लंब खींचिए । स्पष्टत:
लंब खींचिए । स्पष्टत: 



 हैं तथा इन तीन लंबों के पाद
हैं तथा इन तीन लंबों के पाद  - तल में स्थित हैं बिंदु
- तल में स्थित हैं बिंदु  ,
,  और
और  उस रेखा पर स्थित हैं जो उस तल और
उस रेखा पर स्थित हैं जो उस तल और  - तल के प्रतिच्छेदन से बनती है। बिंदु
- तल के प्रतिच्छेदन से बनती है। बिंदु  से रेखा
से रेखा  के समांतर रेखा
के समांतर रेखा  खींचिए |
खींचिए |  रेखा खींचे गए लंब के तल में स्थित है तथा रेखा
रेखा खींचे गए लंब के तल में स्थित है तथा रेखा  (विस्तारित) को
(विस्तारित) को  और
और  को
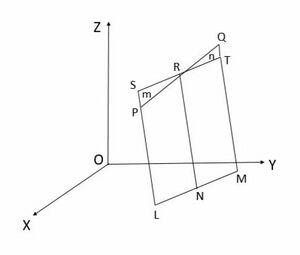
को  पर प्रतिच्छेदित करती है। जैसा चित्र में प्रदर्शित है।
पर प्रतिच्छेदित करती है। जैसा चित्र में प्रदर्शित है।
स्पष्टतः चर्तुभुज  और
और  समांतर चर्तुभुज हैं। त्रिभुजों
समांतर चर्तुभुज हैं। त्रिभुजों  और
और  स्पष्टतः समरूप हैं। इसलिए
स्पष्टतः समरूप हैं। इसलिए

इस प्रकार

ठीक इसी प्रकार  - तल और
- तल और  - तल पर लंब खींचने पर हमें प्राप्त होता है,
- तल पर लंब खींचने पर हमें प्राप्त होता है,
 और
और 
अत: बिंदु  जो बिंदु
जो बिंदु  और
और  को मिलाने वाले रेखा खंड को
को मिलाने वाले रेखा खंड को  के अनुपात में अंत: विभाजित करता है, के निर्देशांक हैं,
के अनुपात में अंत: विभाजित करता है, के निर्देशांक हैं,

यदि बिंदु  , रेखा खंड
, रेखा खंड  को
को  अनुपात में बाह्य विभाजित करता हो तो इसके निर्देशांक उपर्युक्त सूत्र में
अनुपात में बाह्य विभाजित करता हो तो इसके निर्देशांक उपर्युक्त सूत्र में  को
को  से विस्थापित करके प्राप्त किए जाते हैं। इस प्रकार
से विस्थापित करके प्राप्त किए जाते हैं। इस प्रकार  के निर्देशांक होंगें,
के निर्देशांक होंगें,

स्थिति-1 मध्य-बिंदु के निर्देशांक यदि  , रेखाखंड
, रेखाखंड  का मध्य-बिंदु है तो
का मध्य-बिंदु है तो  रखने पर
रखने पर
 ,
,  और
और 
ये  और
और  को मिलाने वाली रेखा खंड के मध्य-बिंदु के निर्देशांक हैं।
को मिलाने वाली रेखा खंड के मध्य-बिंदु के निर्देशांक हैं।
स्थिति-2 रेखा खंड  को
को  के अनुपात में अंतः विभाजित करने वाले बिंदु
के अनुपात में अंतः विभाजित करने वाले बिंदु  के निर्देशांक
के निर्देशांक  रखने पर प्राप्त किए जा सकते हैं:
रखने पर प्राप्त किए जा सकते हैं:

यह परिणाम प्रायः दो बिंदुओं को मिलाने वाली रेखा पर व्यापक बिंदु संबंधी प्रश्नों के हल करने में प्रयुक्त होता है।