समरूप आकृतियाँ
समरूप आकृतियाँ दो आकृतियाँ होती हैं जिनका आकार एक जैसा होता है। जो वस्तुएँ बिल्कुल एक ही आकार और माप की होती हैं, उन्हें सर्वांगसम वस्तुएँ कहा जाता है। उदाहरण के लिए, वास्तविक जीवन में, आप देखेंगे कि कार के दोनों अगले पहिये, किसी व्यक्ति के दोनों हाथ इत्यादि सर्वांगसम आकृतियों या वस्तुओं के उदाहरण हैं। लेकिन समरूप आकृति वाली वस्तुओं का आकार तो एक जैसा होता है लेकिन उनके माप भिन्न-भिन्न होते हैं।
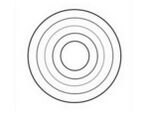
कुछ ज्यामितीय आकृतियाँ या चित्र हमेशा प्रकृति में समान होती हैं। किसी एक वृत्त पर विचार करें, यदि वृत्त की त्रिज्या बदलती रहती है, तो भी इसका आकार वही रहता है। इसलिए, यह कहा जा सकता है कि विभिन्न त्रिज्या वाले सभी वृत्त एक-दूसरे के समान होते हैं। चित्र-1 उन संकेंद्रित वृत्तों को दर्शाता है जिनकी त्रिज्याएँ भिन्न हैं लेकिन वे सभी समान हैं।
हालाँकि इन वृत्तों का आकार एक जैसा है लेकिन इनके माप भिन्न-भिन्न हैं और इसलिए ये सर्वांगसम नहीं हैं।
समरूप आकृतियाँ- परिभाषा
गणित की दृष्टि से, जब दो आकृतियों का आकार एक जैसा होता है लेकिन उनके माप अलग-अलग होते हैं, तो ऐसी आकृतियों को समरूप आकृतियाँ कहा जाता है। उदाहरण के लिए, किसी व्यक्ति की अलग-अलग माप की तस्वीरें यानी स्टाम्प साइज़, पासपोर्ट साइज़ आदि समरूप वस्तुओं को दर्शाती हैं लेकिन वे सर्वांगसम नहीं होती हैं। ज्यामिति में, दो समरूप आकृतियाँ जैसे समान त्रिभुज, समान आयत, समान वर्ग, ऐसी आकृतियाँ हैं जिनके आयाम समान या सामान्य अनुपात में हैं लेकिन उनकी भुजाओं का माप या लंबाई भिन्न-भिन्न होती है जैसा कि चित्र-2 में दिखाया गया है। सार्व अनुपात को स्केल गुणक कहा जाता है। साथ ही, संगत कोण माप में समान होते हैं।
समरूप आकृतियाँ- उदाहरण
यह ध्यान में रखना होगा कि जब भी हम समरूप आकृतियों के बारे में बात करते हैं, तो हम केवल उनके आकार पर विचार करते हैं, चाहे उनका माप कुछ भी हो। इस प्रकार हम यह निष्कर्ष निकाल सकते हैं कि सभी समरूप आकृतियाँ समान हैं, लेकिन सभी समान आकृतियाँ समरूप नहीं हैं।
यदि हम सभी समरूप आकृतियों का अवलोकन करें, तो हम देख सकते हैं कि किसी भी n-पक्षीय बहुभुज के लिए, प्रत्येक रेखाखंड के झुकाव कोण प्रायः समान होते हैं, चाहे आकृति का माप कुछ भी हो। इस प्रकार भुजाओं की समान संख्या वाले किन्हीं दो n-भुजाओं वाले बहुभुजों के लिए, यह कहा जा सकता है कि वे समरूप हैं यदि,
- दोनों बहुभुजों के संगत कोण समान हैं, तथा
- दोनों बहुभुजों की संगत भुजाओं का अनुपात समान है।