परिचय
समुच्चयों का अंतर महत्वपूर्ण और मौलिक समुच्चय सिद्धांत संक्रियाओं में से एक है। समुच्चयों के अंतर के अलावा संघ और प्रतिच्छेदन अन्य समुच्चय सिद्धांत संक्रियाएँ हैं। दो समुच्चयों  और
और  का अंतर फिर से एक समुच्चय है जिसमें
का अंतर फिर से एक समुच्चय है जिसमें  के तत्व उपस्थित हैं जो
के तत्व उपस्थित हैं जो  में नहीं हैं।
में नहीं हैं।
इस लेख में, आइए समुच्चयों के अंतर, उनके गुणों के साथ-साथ वेन आरेखों और हल किए गए उदाहरणों के बारे में अधिक जानें।
परिभाषा
समुच्चयों  और
और  का अंतर उन अवयवों का समुच्चय है जो
का अंतर उन अवयवों का समुच्चय है जो  में हैं किंतु
में हैं किंतु  में नहीं हैं, जब कि
में नहीं हैं, जब कि  और
और  को इसी क्रम में लिया जाए। प्रतीतात्मक रूप में इसे
को इसी क्रम में लिया जाए। प्रतीतात्मक रूप में इसे  लिखते हैं और “
लिखते हैं और “ अंतर
अंतर  ” पढ़ते हैं।
” पढ़ते हैं।
उदाहरण
उदाहरण 1: मान लेते हैं कि  ,
,  तब
तब  और
और  ज्ञात कीजिए ।
ज्ञात कीजिए ।
हल हम प्राप्त करते हैं कि, , क्योंकि अवयव
, क्योंकि अवयव  समुच्चय
समुच्चय  में हैं किंतु
में हैं किंतु  में नहीं हैं तथा
में नहीं हैं तथा  , क्योंकि अवयव
, क्योंकि अवयव  ,
,  में है किंतु
में है किंतु  में नहीं है। हम देखते हैं कि
में नहीं है। हम देखते हैं कि 
उदाहरण 2: मान लीजिए कि  तो
तो  , तो
, तो  और
और  ज्ञात कीजिए।
ज्ञात कीजिए।
हल यहाँ,  , क्योंकि अवयव
, क्योंकि अवयव  समुच्चय
समुच्चय  में हैं किंतु
में हैं किंतु  में नहीं है तथा -
में नहीं है तथा -  , क्योंकि अवयव
, क्योंकि अवयव  समुच्चय
समुच्चय  में है परंतु
में है परंतु  में नहीं है।
में नहीं है।
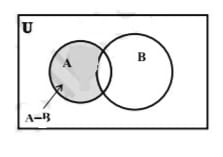
चित्र-1 समुच्चयों का अंतर
हम यह अवश्य ध्यान देते हैं कि  समुच्चय निर्माण संकेतन का प्रयोग करते हुए हम समुच्चयों के अंतर की परिभाषा को पुनः इस प्रकार लिख सकते हैं:
समुच्चय निर्माण संकेतन का प्रयोग करते हुए हम समुच्चयों के अंतर की परिभाषा को पुनः इस प्रकार लिख सकते हैं:
 और
और 
दो समुच्चयों  और
और  के अंतर को वेन आरेख द्वारा दर्शाया जा सकता है जैसा कि चित्र-1 में प्रदर्शित है। छायांकित भाग दो समुच्चय
के अंतर को वेन आरेख द्वारा दर्शाया जा सकता है जैसा कि चित्र-1 में प्रदर्शित है। छायांकित भाग दो समुच्चय  और
और  के अंतर को दर्शाता है।
के अंतर को दर्शाता है।
समुच्चयों के अंतर के गुणधर्म
किसी भी दो समुच्चयों A और B के लिए, यहाँ समुच्चयों के अंतर के गुण दिए गए हैं। यहाँ, ∅ रिक्त समुच्चय को दर्शाता है।




 यदि
यदि 
 यदि
यदि 
- यदि
 , तब
, तब 


टिप्पणी
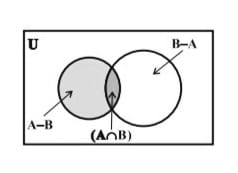
चित्र-2 समुच्चयों का अंतर
समुच्चय  और
और  परस्पर असंयुक्त होते हैं अर्थात् इनमें से किसी दो समुच्चयों का सर्वनिष्ठ समुच्चय एक रिक्त समुच्चय होता है जैसा कि चित्र-2 में प्रदर्शित है।
परस्पर असंयुक्त होते हैं अर्थात् इनमें से किसी दो समुच्चयों का सर्वनिष्ठ समुच्चय एक रिक्त समुच्चय होता है जैसा कि चित्र-2 में प्रदर्शित है।

