गणितीय आगमन का सिद्धांत: Difference between revisions

Latest revision as of 10:20, 11 November 2024

परिचय

गणित में आगमन का उपयोग किसी प्रमाण और निष्कर्ष पर पहुँचने के लिए किया जाता है, जो गणितीय सिद्धांतों और उदाहरणों को समझने में मदद करता है। समाधान की इस लेख में गणितीय आगमन के सिद्धांत के विभिन्न गुणों और अवधारणाओं को विस्तार से समझाया गया है, जो सैद्धांतिक गणित की नींव रखते हैं।

गणितीय चिंतन का एक आधारभूत सिद्धांत निगमनिक तर्क है। तर्कशास्त्र के अध्ययन से उद्धृत एक अनौपचारिक और निगमनिक तर्क का उदाहरण तीन कथनों में व्यक्त तर्क है:-

(a) सुकरात एक मनुष्य है।

(b) सभी मनुष्य मरणशील हैं, इसलिए,

(c) सुकरात मरणशील है।

यदि कथन (a) और (b) सत्य हैं, तो (c) की सत्यता स्थापित है। इस सरल उदाहरण को गणितीय बनाने के लिए हम लिख सकते हैं।

आठ दो से भाज्य है।
दो से भाज्य कोई संख्या सम संख्या है, इसलिए,
आठ एक सम संख्या है।

इस प्रकार संक्षेप में निगमन एक प्रक्रिया है जिसमें एक कथन सिद्ध करने को दिया जाता है, जिसे गणित में प्राय: एक अनुमानित कथन (कंजेक्चर) अथवा प्रमेय कहते हैं, तर्क संगत निगमन के चरण प्राप्त किए जाते हैं और एक उपपत्ति स्थापित की जा सकती है, अथवा नहीं की जा सकती है, अर्थात् निगमन व्यापक स्थिति से विशेष स्थिति प्राप्त करने का अनुप्रयोग है।

निगमन के विपरीत, आगमन तर्क प्रत्येक स्थिति के अध्ययन पर आधारित होता है तथा इसमें प्रत्येक एवं हर संभव स्थिति को ध्यान में रखते हुए घटनाओं के निरीक्षण द्वारा एक अनुमानित कथन विकसित किया जाता है। इसको गणित में प्रायः प्रयोग किया जाता है तथा वैज्ञानिक चिंतन, जहाँ आँकड़ों का संग्रह तथा विशलेषण मानक होता है, का यह मुख्य आधार है। इस प्रकार, सरल भाषा में हम कह सकते हैं कि आगमन शब्द का अर्थ विशिष्ट स्थितियों या तथ्यों से व्यापकीकरण करने से है।

बीजगणित में या गणित की अन्य शाखाओं में, कुछ ऐसे परिणाम या कथन होते हैं जिन्हें एक धन पूर्णांक $'n'$ के पदों में व्यक्त किया जाता है। ऐसे कथनों को सिद्ध करने के लिए विशिष्ट तकनीक पर आधारित समुचित सिद्धांत है जो गणितीय आगमन का सिद्धांत (प्रिंसिपल ऑफ मैथमेटिकल इंडक्शन) कहलाता है।

हम जानते हैं कि प्राकृत संख्याओं का समुच्चय $N$ वास्तविक संख्याओं का विशेष क्रमित उपसमुच्चय है। वास्तव में, $R$ का सबसे छोटा उपसमुच्चय $N$ है, जिसमें निम्नलिखित गुण हैं:

एक समुच्चय $S$ आगमनिक समुच्चय (इंडक्टिव सेट) कहलाता है यदि $1\in S$ और $x+1\in S$ जब कभी $x\in S$ । क्योंकि $N$ , जो कि एक आगमनिक समुच्चय है, $R$ का सबसे छोटा उपसमुच्चय है, परिणामत: $R$ के किसी भी ऐसे उपसमुच्चय में जो आगमनिक है, $N$ अनिवार्य रूप से समाहित होता है।

गणितीय आगमन

गणितीय आगमन एल्गोरिथ्म में दिए गए कथनों को सामान्यीकृत करने या विशेष स्थितियों से सामान्यीकृत करने की एक विशेष विधि या तकनीक है। यह निगमन विधि के विपरीत है। यहाँ हम हर स्थिति पर काम करते हैं और हर स्थितियों का अवलोकन करते हैं और फिर सिद्ध करते हैं कि दिया गया कथन सभी स्थितियों के लिए सत्य है। इन कथनों को सिद्ध करने के लिए हम कुछ सिद्धांतों का उपयोग करते हैं जिन्हें गणितीय आगमन का सिद्धांत कहा जाता है।

चित्र -1 गणितीय आगमन

गणित में, हम सम्पूर्ण आगमन का एक रूप जिसे गणितीय आगमन कहते हैं, प्रयुक्त करते हैं। गणितीय आगमन सिद्धांत के मूल को समझने के लिए, कल्पना कीजिए कि एक पतली आयताकार टाइलों का समूह एक सिरे पर रखा है, जैसे चित्र-1 में प्रदर्शित है।

मान लीजिए, हमारे पास आयताकार टाइलों का एक समुच्चय है और हम आयताकार टाइलों को इस तरह से रखते हैं कि अगर हम पहले आयताकार टाइल को धक्का देते हैं तो सभी आयताकार टाइलें गिर जाएँगी। अगर हम इस बारे में सुनिश्चित होना चाहते हैं, तो हमें यह सिद्ध करना होगा कि

• पहला आयताकार टाइल गिरता है

• अगर कोई भी आयताकार टाइल गिरता है तो उसका अगला आयताकार टाइल या उत्तरवर्ती अनिवार्यतः निश्चित रूप से गिर जाएगा।

अगर उपरोक्त दोनों कथन सत्य सिद्ध होते हैं तो हम कह सकते हैं कि अगर हम एक आयताकार टाइलों को धक्का देते हैं तो सभी आयताकार टाइलें गिर जाएँगी।

गणितीय आगमन का सिद्धांत

उपर्युक्त अवधारणा गणितीय आगमन के सिद्धांत को प्राप्त करती है जिसका उपयोग $n$ प्राकृतिक संख्याओं के संदर्भ में दिए गए कथनों को सीधे सिद्ध करने के लिए किया जाता है।

• आधार स्थिति: दिया गया कथन पहली $n$ प्राकृतिक संख्या के लिए सही है, अर्थात $n=1$ के लिए, $p(1)$ सत्य है।

• आगमनात्मक चरण: यदि दिया गया कथन $n=k$ जैसी किसी भी प्राकृतिक संख्या के लिए सही है तो यह $n=k+1$ के लिए भी सही होगा, अर्थात यदि $p(k)$ सत्य है तो $p(k+1)$ भी सत्य है।

यह सिद्धांत कहता है कि यदि उपरोक्त दोनों चरण सिद्ध हो जाते हैं तो $p(n)$ सभी प्राकृतिक संख्याओं के लिए सत्य है। उदाहरण

आइए $n\geq 0$ के लिए पहले $n$ वर्गों के योग के सूत्र का उदाहरण लें। हम $n$ प्राकृतिक संख्याओं के वर्गों के योग में एक पैटर्न पाएँगे:

$0^{2}=0$

$0^{2}+1^{2}=1$

$0^{2}+1^{2}+2^{2}=5$

$0^{2}+1^{2}+2^{2}+3^{2}=14$

यदि हम इस प्रतिरूप(पैटर्न) का अनुसरण करते हैं तो हम देख सकते हैं कि पहले $n$ वर्गों का योग $n(n+1)(2n+1)/6$ हो सकता है। अब हमें यह सिद्ध करना है कि यह सूत्र प्रत्येक संख्या $n\geq 0$ के लिए कार्य करता है, अर्थात् हमें अनंत संख्या में समानताएँ सिद्ध करनी हैं।

अब हम इसे गणितीय आगमन के सिद्धांत से सिद्ध करने का प्रयास करेंगे।

चरण 1 सबसे पहले हमें यह जानना चाहिए कि पहले $n$ वर्गों का योग बराबर है

${\frac {n(n+1)(2n+1)}{6}}$ सभी $n\geq 0$ के लिए

चरण 2 किसी भी $n\geq 0$ के लिए, मान लें कि $p(n)$ यह प्रस्ताव है कि

$0^{2}+1^{2}+2^{2}+3^{2}+......+(n-1)^{2}+n^{2}={\frac {n(n+1)(2n+1)}{6}}$

हमें यह दिखाना है कि $p(n)$ सभी $n\geq 0$ के लिए सत्य है।

चरण 3 आधार मामले में, $n=0$ लें। हम दिखाएंगे कि $p(0)$ सत्य है: अर्थात,

$0^{2}+....+0^{2}={\frac {0(0+1)(2.0+1)}{6}}$ ( $n=0$ का मान रखकर)

$0^{2}+....+0^{2}=0={\frac {0(0+1)(0+1)}{6}}$

बाएं पक्ष = दायां पक्ष

आगमन परिकल्पना के लिए, मान लें कि $p(k)$ , $k\geq 0$ के लिए सत्य है। यानी, मान लें कि

$0^{2}+1^{2}+2^{2}+......+(k-1)^{2}+k^{2}={\frac {k(k+1)(2k+1)}{6}}$

चरण 4 अब हम उपरोक्त धारणा कि $p(k)$ सत्य है, का प्रयोग करके सिद्ध करेंगे कि $p(k+1)$ सत्य है। तो हम सिद्ध करेंगे कि

$0^{2}+1^{2}+2^{2}+......+k^{2}+(k+1)^{2}={\frac {(k+1)(k+2)(2(k+1)+1)}{6}}$

$={\frac {(k+1)(k+2)(2k+3)}{6}}$

चरण 5 यह साबित करता है कि $p(k+1)$ सत्य है यदि $p(k)$ इस प्रकार सत्य है:

बाएं हाथ की ओर

$=0^{2}+1^{2}+2^{2}+......+k^{2}+(k+1)^{2}$

$=(0^{2}+1^{2}+2^{2}+......+k^{2})+(k+1)^{2}$

$={\frac {k(k+1)(2k+1)}{6}}+(k+1)^{2}$ (आगमन परिकल्पना $p(k)$ द्वारा)

${\frac {k(k+1)(2k+1)+6(k+1)^{2}}{6}}$ (बीजगणित द्वारा)

$={\frac {(k+1)(2k^{2}+k)+(k+1)(6k+6)}{6}}$

$={\frac {(k+1)(k+2)(2k+3)}{6}}$

= दायाँ पक्ष।

अतः, यदि $p(k)$ सत्य है, तो $p(k+1)$ भी सत्य है, किसी भी $k\geq 0$ के लिए।

चरण 6 उपरोक्त चरणों ने प्रदर्शित किया कि किसी भी $k\geq 0$ के लिए, यदि $p(k)$ सत्य है, तो $p(k+1)$ भी सत्य है और $p(0)$ भी आधार मामले के अनुसार सत्य है, इसलिए जब उपरोक्त दोनों चरण सिद्ध हो जाते हैं, तो यह दर्शाता है कि $n\geq 0$ के लिए, $p(n)$ सत्य है, जैसा कि आवश्यक है।

गणितीय आगमन का उपयोग

हम गणितीय आगमन का उपयोग कब कर सकते हैं?

गणितीय आगमन का उपयोग इतने सारे कथनों के लिए किया जा सकता है जहाँ हम यह दिखाना चाहते हैं कि कथन सत्य है। इस नई तकनीक से हर कथन को सिद्ध नहीं किया जा सकता है।

• सबसे पहले, आगमन में हमें सभी पूर्णांकों $n\geq 0$ के लिए अपना कथन $p(n)$ ज्ञात करना होगा, इसलिए आगमन केवल पूर्ण संख्याओं वाले कथनों के साथ काम करता है। इसलिए, "सभी $x\in R$ के लिए, $x^{2}\geq 0$ " जैसे कथन आगमन के साथ सिद्ध नहीं हो पाएंगे क्योंकि वास्तविक संख्याओं के सेट की गणना करना आसान नहीं है।

• दूसरे, हमारे आगमन प्रमाण के लिए हमें प्रेरक चरण का पालन करना होगा, अर्थात, कथन जहाँ t $p(k+1)$ मामला सत्य है, यह मानते हुए कि $p(k)$ मामला सत्य है, आगमन के लिए विशेष रूप से उपयुक्त हैं। उदाहरण के लिए, योगों से जुड़े कथन उपयुक्त हैं क्योंकि कथन $p(k+1)$ के बाएँ हाथ के हिस्से को कथन $p(k)$ के बाएँ हाथ के हिस्से के संदर्भ में लिखना आसान है।

@@ Line 12: / Line 12: @@
 यदि कथन (a) और (b) सत्य हैं, तो (c) की सत्यता स्थापित है। इस सरल उदाहरण को गणितीय बनाने के लिए हम लिख सकते हैं।
-(i) आठ दो से भाज्य है।
+# आठ दो से भाज्य है।
+# दो से भाज्य कोई संख्या सम संख्या है, इसलिए,
-(ii) दो से भाज्य कोई संख्या सम संख्या है, इसलिए,
+# आठ एक सम संख्या है।
-(iii) आठ एक सम संख्या है।
 इस प्रकार संक्षेप में निगमन एक प्रक्रिया है जिसमें एक कथन सिद्ध करने को दिया जाता है, जिसे गणित में प्राय: एक अनुमानित कथन (कंजेक्चर) अथवा प्रमेय कहते हैं, तर्क संगत निगमन के चरण प्राप्त किए जाते हैं और एक उपपत्ति स्थापित की जा सकती है, अथवा नहीं की जा सकती है, अर्थात् निगमन व्यापक स्थिति से विशेष स्थिति प्राप्त करने का अनुप्रयोग है।
@@ Line 24: / Line 22: @@
 बीजगणित में या गणित की अन्य शाखाओं में, कुछ ऐसे परिणाम या कथन होते हैं जिन्हें एक धन पूर्णांक <math>'n'</math> के पदों में व्यक्त किया जाता है। ऐसे कथनों को सिद्ध करने के लिए विशिष्ट तकनीक पर आधारित समुचित सिद्धांत है जो गणितीय आगमन का सिद्धांत (प्रिंसिपल ऑफ मैथमेटिकल इंडक्शन) कहलाता है।
-हम जानते हैं कि प्राकृत संख्याओं का समुच्चय <math>N</math> वास्तविक संख्याओं का विशेष क्रमित उपसमुच्चय है। वास्तव में, <math>R</math> का सबसे छोटा उपसमुच्चय <math>N</math> है, जिसमें निम्नलिखित गुण हैं:
+हम जानते हैं कि प्राकृत संख्याओं का समुच्चय <math>N</math> [[वास्तविक संख्याओं पर संक्रियाएँ|वास्तविक संख्याओं]] का विशेष क्रमित उपसमुच्चय है। वास्तव में, <math>R</math> का सबसे छोटा उपसमुच्चय <math>N</math> है, जिसमें निम्नलिखित गुण हैं:
-एक समुच्चय <math>S</math> आगमनिक समुच्चय (इंडक्टिव सेट) कहलाता है यदि <math>1\in S </math> और <math>x+1\in S </math> जब कभी <math>x\in S</math> ।   क्योंकि <math>N</math>, जो कि एक आगमनिक समुच्चय है, <math>R</math> का सबसे छोटा उपसमुच्चय है, परिणामत: <math>R</math> के किसी भी ऐसे उपसमुच्चय में जो आगमनिक है, <math>N</math> अनिवार्य रूप से समाहित होता है।
+एक [[समुच्चय]] <math>S</math> आगमनिक समुच्चय (इंडक्टिव सेट) कहलाता है यदि <math>1\in S </math> और <math>x+1\in S </math> जब कभी <math>x\in S</math> ।   क्योंकि <math>N</math>, जो कि एक आगमनिक समुच्चय है, <math>R</math> का सबसे छोटा उपसमुच्चय है, परिणामत: <math>R</math> के किसी भी ऐसे उपसमुच्चय में जो आगमनिक है, <math>N</math> अनिवार्य रूप से समाहित होता है।
 == गणितीय आगमन ==
 गणितीय आगमन एल्गोरिथ्म में दिए गए कथनों को सामान्यीकृत करने या विशेष स्थितियों से सामान्यीकृत करने की एक विशेष विधि या तकनीक है। यह निगमन विधि के विपरीत है। यहाँ हम हर स्थिति पर काम करते हैं और हर स्थितियों का अवलोकन करते हैं और फिर सिद्ध करते हैं कि दिया गया कथन सभी स्थितियों के लिए सत्य है। इन कथनों को सिद्ध करने के लिए हम कुछ सिद्धांतों का उपयोग करते हैं जिन्हें गणितीय आगमन का सिद्धांत कहा जाता है।
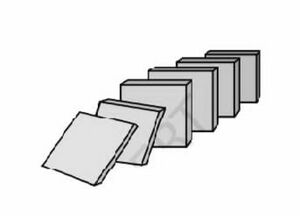
+[[File:गणितीय आगमन.jpg|thumb|चित्र -1 गणितीय आगमन]]
 गणित में, हम सम्पूर्ण आगमन का एक रूप जिसे गणितीय आगमन कहते हैं, प्रयुक्त करते हैं। गणितीय आगमन सिद्धांत के मूल को समझने के लिए, कल्पना कीजिए कि एक पतली आयताकार टाइलों का समूह एक सिरे पर रखा है, जैसे चित्र-1 में प्रदर्शित है।
@@ Line 44: / Line 42: @@
 उपर्युक्त अवधारणा गणितीय आगमन के सिद्धांत को प्राप्त करती है जिसका उपयोग <math>n </math> प्राकृतिक संख्याओं के संदर्भ में दिए गए कथनों को सीधे सिद्ध करने के लिए किया जाता है।
-• '''आधार स्थिति:''' दिया गया कथन पहली <math>n </math> प्राकृतिक संख्या के लिए सही है, अर्थात <math>n=1</math> के लिए, <math>p(1)</math> सत्य है।
+• '''आधार स्थिति:''' दिया गया कथन पहली <math>n </math> [[प्राकृतिक संख्याएँ|प्राकृतिक संख्या]] के लिए सही है, अर्थात <math>n=1</math> के लिए, <math>p(1)</math> सत्य है।
 • '''आगमनात्मक चरण:''' यदि दिया गया कथन <math>n=k</math> जैसी किसी भी प्राकृतिक संख्या के लिए सही है तो यह <math>n=k+1</math> के लिए भी सही होगा, अर्थात यदि <math>p(k)</math> सत्य है तो <math>p(k+1)</math>भी सत्य है।
@@ Line 62: / Line 60: @@
 यदि हम इस  प्रतिरूप(पैटर्न) का अनुसरण करते हैं तो हम देख सकते हैं कि पहले <math>n </math> वर्गों का योग <math>n(n+1)(2n+1)/6</math> हो सकता है। अब हमें यह सिद्ध करना है कि यह सूत्र प्रत्येक संख्या <math>n\geq 0</math> के लिए कार्य करता है, अर्थात् हमें अनंत संख्या में समानताएँ सिद्ध करनी हैं।
+अब हम इसे गणितीय आगमन के सिद्धांत से सिद्ध करने का प्रयास करेंगे।
+'''चरण 1''' सबसे पहले हमें यह जानना चाहिए कि पहले <math>n </math> वर्गों का योग बराबर है
+<math>\frac{n(n+1)(2n+1)}{6}</math> सभी <math>n\geq 0</math> के लिए
-अब हम इसे गणितीय आगमन के सिद्धांत से सिद्ध करने का प्रयास करेंगे। चरण 1. सबसे पहले हमें यह जानना चाहिए कि पहले n वर्गों का योग बराबर है
+'''चरण 2''' किसी भी <math>n\geq 0</math> के लिए, मान लें कि <math>p(n)</math> यह प्रस्ताव है कि
-n (n + 1) (2n + 1) सभी n ≥ 0 के लिए
-चरण 2. किसी भी n ≥ 0 के लिए, मान लें कि P (n) यह प्रस्ताव है कि
-+12+22+32 + ·
+<math>0^2+1^2+2^2+3^2+......+(n-1)^2+n^2=\frac{n(n+1)(2n+1)}{6}</math>
-· · · · + (n − 1)2 + n 2 = n (n + 1) (2n + 1)
+हमें यह दिखाना है कि <math>p(n)</math> सभी <math>n\geq 0</math> के लिए सत्य है।
-हमें यह दिखाना है कि P (n) सभी n ≥ 0 के लिए सत्य है।
+'''चरण 3''' आधार मामले में, <math>n=0</math> लें। हम दिखाएंगे कि <math>p(0)</math> सत्य है: अर्थात,
-चरण 3. आधार मामले में, n = 0 लें। हम दिखाएंगे कि P (0) सत्य है: अर्थात,
+<math>0^2+....+0^2=\frac{0(0+1)(2.0+1)}{6}</math> (<math>n=0 </math> का मान रखकर)
-++02=0(0+1) (2 - 0 + 1) (n का मान = 0 रखकर)
+<math>0^2+....+0^2=0=\frac{0(0+1)(0+1)}{6} </math>
-++02 = 0 = 0(0+1) (0+1)/6
 बाएं पक्ष = दायां पक्ष
-प्रेरण परिकल्पना के लिए, मान लें कि p (k) k≥0 के लिए सत्य है। यानी, मान लें कि
+आगमन परिकल्पना के लिए, मान लें कि <math>p(k)</math>, <math>k\geq 0 </math> के लिए सत्य है। यानी, मान लें कि
-+12+22++ (k-1)2 + k 2 = k (k + 1) (2k + 1)
+<math>0^2+1^2+2^2+......+(k-1)^2+k^2=\frac{k(k+1)(2k+1)}{6} </math>
-चरण 4. अब हम उपरोक्त धारणा कि P(k) सत्य है, का प्रयोग करके सिद्ध करेंगे कि P(k + 1) सत्य है। तो हम साबित करेंगे कि
-+ 12 +22+ · +k2+(k+1)2 = (k + 1) (k + 2) (2(k + 1) + 1)
+'''चरण 4''' अब हम उपरोक्त धारणा कि <math>p(k)</math> सत्य है, का प्रयोग करके सिद्ध करेंगे कि <math>p(k+1) </math> सत्य है। तो हम सिद्ध करेंगे कि
-=
+<math>0^2+1^2+2^2+......+k^2+(k+1)^2=\frac{(k+1)(k+2)(2(k+1)+1)}{6}  </math>
+<math>=\frac{(k+1)(k+2)(2k+3)}{6}  </math>
-= (k + 1)(k + 2)(2k + 3)
+'''चरण 5''' यह साबित करता है कि <math>p(k+1) </math> सत्य है यदि <math>p(k)</math> इस प्रकार सत्य है:
-चरण 5. यह साबित करता है कि p (k+1) सत्य है यदि p (k) इस प्रकार सत्य है:
 बाएं हाथ की ओर
-=02+12+22+
+<math>= 0^2+1^2+2^2+......+k^2+(k+1)^2 </math>
-= (02 + 12 +22+
+<math>= (0^2+1^2+2^2+......+k^2)+(k+1)^2 </math>
-+ k2 +(k+1)2
+<math>= \frac{k(k+1)(2k+1)}{6} +(k+1)^2 </math>  (आगमन परिकल्पना <math>p(k)</math> द्वारा)
-+ k2) + (k + 1)2
+<math>\frac{k(k+1)(2k+1)+6(k+1)^2}{6} </math>(बीजगणित द्वारा)
-= k (k + 1) (2k + 1)+(k+1)2 (प्रेरण परिकल्पना P (k) द्वारा) 6
+<math>=\frac{(k+1)(2k^2+k)+(k+1)(6k+6)}{6} </math>
-= k (k + 1) (2k + 1) + 6(k + 1)2 (बीजगणित द्वारा)
+<math>=\frac{(k+1)(k+2)(2k+3)}{6} </math>
-=
+= दायाँ पक्ष।
+अतः, यदि <math>p(k)</math> सत्य है, तो <math>p(k+1) </math> भी सत्य है, किसी भी <math>k\geq 0 </math> के लिए।
-= (k + 1) (2k 2 + k) + (k + 1) (6k+6)
-= (k+1) (2k 2 + 7k+6)
-= (k + 1) (k + 2) (2k + 3)
-= दायाँ पक्ष।
-अतः, यदि P (k) सत्य है, तो P (k+1) भी सत्य है, किसी भी k≥ 0 के लिए।
+'''चरण 6''' उपरोक्त चरणों ने प्रदर्शित किया कि किसी भी <math>k\geq 0 </math> के लिए, यदि <math>p(k)</math> सत्य है, तो <math>p(k+1) </math> भी सत्य है और <math>p(0)</math> भी आधार मामले के अनुसार सत्य है, इसलिए जब उपरोक्त दोनों चरण सिद्ध हो जाते हैं, तो यह दर्शाता है कि <math>n\geq 0</math> के लिए, <math>p(n)</math> सत्य है, जैसा कि आवश्यक है।
-चरण 6. उपरोक्त चरणों ने प्रदर्शित किया कि किसी भी k ≥ 0 के लिए, यदि P(k) सत्य है, तो P(k + 1) भी सत्य है और P(0) भी आधार मामले के अनुसार सत्य है, इसलिए जब उपरोक्त दोनों चरण सिद्ध हो जाते हैं, तो यह दर्शाता है कि al > 0 के लिए, P(n) सत्य है, जैसा कि आवश्यक है।
+== गणितीय आगमन का उपयोग ==
+हम गणितीय आगमन का उपयोग कब कर सकते हैं?
-== हम गणितीय प्रेरण का उपयोग कब कर सकते हैं? ==
+गणितीय आगमन का उपयोग इतने सारे कथनों के लिए किया जा सकता है जहाँ हम यह दिखाना चाहते हैं कि कथन सत्य है। इस नई तकनीक से हर कथन को सिद्ध नहीं किया जा सकता है।
-गणितीय प्रेरण का उपयोग इतने सारे कथनों के लिए किया जा सकता है जहाँ हम यह दिखाना चाहते हैं कि कथन सत्य है। इस नई तकनीक से हर कथन को सिद्ध नहीं किया जा सकता है।
-• सबसे पहले, प्रेरण में हमें सभी पूर्णांकों n ≥ 0 के लिए अपना कथन P (n) ज्ञात करना होगा, इसलिए प्रेरण केवल पूर्ण संख्याओं वाले कथनों के साथ काम करता है। इसलिए, "सभी x e R के लिए, x2 ≥ 0" जैसे कथन प्रेरण के साथ सिद्ध नहीं हो पाएंगे क्योंकि वास्तविक संख्याओं के सेट की गणना करना आसान नहीं है।
+• सबसे पहले, आगमन में हमें सभी पूर्णांकों <math>n\geq 0</math> के लिए अपना कथन <math>p(n)</math> ज्ञात करना होगा, इसलिए आगमन केवल पूर्ण संख्याओं वाले कथनों के साथ काम करता है। इसलिए, "सभी <math>x\in R</math> के लिए, <math>x^2\geq 0</math>" जैसे कथन आगमन के साथ सिद्ध नहीं हो पाएंगे क्योंकि वास्तविक संख्याओं के सेट की गणना करना आसान नहीं है।
-• दूसरे, हमारे प्रेरण प्रमाण के लिए हमें प्रेरक चरण का पालन करना होगा, अर्थात, कथन जहाँ t P (k + 1) मामला सत्य है, यह मानते हुए कि P (k) मामला सत्य है, प्रेरण के लिए विशेष रूप से उपयुक्त हैं। उदाहरण के लिए, योगों से जुड़े कथन उपयुक्त हैं क्योंकि कथन P (k + 1) के बाएँ हाथ के हिस्से को कथन P (k) के बाएँ हाथ के हिस्से के संदर्भ में लिखना आसान है।
+• दूसरे, हमारे आगमन प्रमाण के लिए हमें प्रेरक चरण का पालन करना होगा, अर्थात, कथन जहाँ t <math>p(k+1) </math> मामला सत्य है, यह मानते हुए कि <math>p(k)</math>मामला सत्य है, आगमन के लिए विशेष रूप से उपयुक्त हैं। उदाहरण के लिए, योगों से जुड़े कथन उपयुक्त हैं क्योंकि कथन <math>p(k+1) </math> के बाएँ हाथ के हिस्से को कथन <math>p(k)</math> के बाएँ हाथ के हिस्से के संदर्भ में लिखना आसान है।
 [[Category:गणितीय आगमन का सिद्धांत]][[Category:कक्षा-11]][[Category:गणित]]
 [[Category:गणितीय आगमन का सिद्धांत]][[Category:कक्षा-11]][[Category:गणित]]